题目内容
己知函数f(x)=x2e-x(Ⅰ)求f(x)的极小值和极大值;
(Ⅱ)当曲线y=f(x)的切线l的斜率为负数时,求l在x轴上截距的取值范围.
【答案】分析:(Ⅰ)利用导数的运算法则即可得出f′(x),利用导数与函数单调性的关系及函数的极值点的定义,即可求出函数的极值;
(Ⅱ)利用导数的几何意义即可得到切线的斜率,得出切线的方程,利用方程求出与x轴交点的横坐标,再利用导数研究函数的单调性、极值、最值即可.
解答:解:(Ⅰ)∵f(x)=x2e-x,∴f′(x)=2xe-x-x2e-x=e-x(2x-x2),
令f′(x)=0,解得x=0或x=2,
令f′(x)>0,可解得0<x<2;令f′(x)<0,可解得x<0或x>2,
故函数在区间(-∞,0)与(2,+∞)上是减函数,在区间(0,2)上是增函数.
∴x=0是极小值点,x=2极大值点,又f(0)=0,f(2)=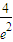 .
.
故f(x)的极小值和极大值分别为0,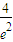 .
.
(II)设切点为(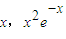 ),
),
则切线方程为y-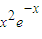 =
=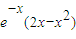 (x-x),
(x-x),
令y=0,解得x=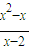 =
=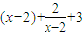 ,
,
因为曲线y=f(x)的切线l的斜率为负数,∴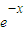 (
(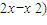 <0,∴x<0或x>2,
<0,∴x<0或x>2,
令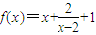 ,
,
则 =
=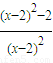 .
.
①当x<0时,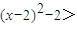 0,即f′(x)>0,∴f(x)在(-∞,0)上单调递增,∴f(x)<f(0)=0;
0,即f′(x)>0,∴f(x)在(-∞,0)上单调递增,∴f(x)<f(0)=0;
②当x>2时,令f′(x)=0,解得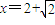 .
.
当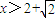 时,f′(x)>0,函数f(x)单调递增;当
时,f′(x)>0,函数f(x)单调递增;当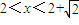 时,f′(x)<0,函数f(x)单调递减.
时,f′(x)<0,函数f(x)单调递减.
故当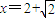 时,函数f(x)取得极小值,也即最小值,且
时,函数f(x)取得极小值,也即最小值,且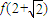 =
=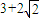 .
.
综上可知:切线l在x轴上截距的取值范围是(-∞,0)∪ .
.
点评:本题考查利用导数求函数的极值与利用导数研究函数的单调性、切线、函数的值域,综合性强,考查了推理能力和计算能力.
(Ⅱ)利用导数的几何意义即可得到切线的斜率,得出切线的方程,利用方程求出与x轴交点的横坐标,再利用导数研究函数的单调性、极值、最值即可.
解答:解:(Ⅰ)∵f(x)=x2e-x,∴f′(x)=2xe-x-x2e-x=e-x(2x-x2),
令f′(x)=0,解得x=0或x=2,
令f′(x)>0,可解得0<x<2;令f′(x)<0,可解得x<0或x>2,
故函数在区间(-∞,0)与(2,+∞)上是减函数,在区间(0,2)上是增函数.
∴x=0是极小值点,x=2极大值点,又f(0)=0,f(2)=
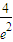 .
.故f(x)的极小值和极大值分别为0,
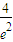 .
.(II)设切点为(
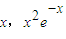 ),
),则切线方程为y-
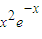 =
=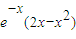 (x-x),
(x-x),令y=0,解得x=
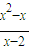 =
=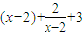 ,
,因为曲线y=f(x)的切线l的斜率为负数,∴
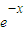 (
(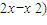 <0,∴x<0或x>2,
<0,∴x<0或x>2,令
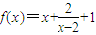 ,
,则
 =
=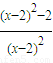 .
.①当x<0时,
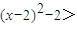 0,即f′(x)>0,∴f(x)在(-∞,0)上单调递增,∴f(x)<f(0)=0;
0,即f′(x)>0,∴f(x)在(-∞,0)上单调递增,∴f(x)<f(0)=0;②当x>2时,令f′(x)=0,解得
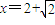 .
.当
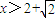 时,f′(x)>0,函数f(x)单调递增;当
时,f′(x)>0,函数f(x)单调递增;当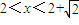 时,f′(x)<0,函数f(x)单调递减.
时,f′(x)<0,函数f(x)单调递减.故当
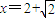 时,函数f(x)取得极小值,也即最小值,且
时,函数f(x)取得极小值,也即最小值,且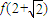 =
=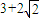 .
.综上可知:切线l在x轴上截距的取值范围是(-∞,0)∪
 .
.点评:本题考查利用导数求函数的极值与利用导数研究函数的单调性、切线、函数的值域,综合性强,考查了推理能力和计算能力.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
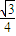 sin x-
sin x- cos x.
cos x.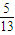 ,x∈[
,x∈[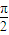 ,π],求函数f (x)的值;
,π],求函数f (x)的值;