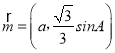Question

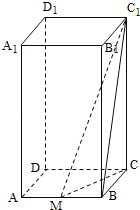
【题目】如图，正四棱柱的底面边长为1，高为2，为线段的中点，求：

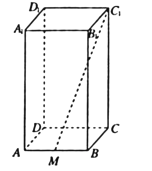
（1）三棱锥的体积；

（2）异面直线与所成角的大小（结果用反三角函数值表示）.

Answer 1

【答案】（1）；（2）（或）

【解析】

（1）连接CM，根据M为AB中点，且正方形ABCD边长为1，得到△BCM的面积为SS正方形ABCD．因为CC1⊥平面ABCD，是三棱锥C1﹣MBC的高，所以利用锥体体积公式，可得三棱锥C1﹣MBC的体积；

（2）连接BC1，正方形ABCD中，因为CD∥AB，所以∠C1MB（或其补角）为异面直线CD与MC1所成的角．Rt△MC1B中，可算出BC1，而MBAB，利用直角三角形中三角函数的定义，得到tan∠C1MB，所以异面直线CD与MC1所成角为arctan．

解：（1）连接CM，

∵正方形ABCD中，M为AB中点，且边长为1，

∴△BCM的面积为SS正方形ABCD．

又∵CC1⊥平面ABCD，

∴CC1是三棱锥C1﹣MBC的高，

∴三棱锥C1﹣MBC的体积为：VC1﹣MBC2；

（2）连接BC1

∵CD∥AB，

∴∠C1MB（或其补角）为异面直线CD与MC1所成的角．

∵AB⊥平面B1C1CB，BC1平面B1C1CB，

∴AB⊥BC1．

Rt△MC1B中，BC1，MBAB

∴tan∠C1MB

所以异面直线CD与MC1所成角为arctan．