题目内容
(本题10分)某家公司每月生产两种布料A和B,所有原料是两种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的总量。
已知生产每匹布料A、B的利润分别为120元、80元。那么如何安排生产才能够产生最大的利润?最大的利润是多少?
| 羊毛颜色 | 每匹需要( kg) | 供应量(kg) | |
| 布料A | 布料B | ||
| 红 | 4 | 4 | 1400 |
| 绿 | 6 | 3 | 1800 |
设每月生产布料A为x 匹、生产布料B为y 匹,利润为Z元,那么
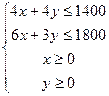 ①; 目标函数为
①; 目标函数为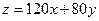 = 40(3 x + 2 y )
= 40(3 x + 2 y )
作出二元一次不等式① 所表示的平面区域(阴影部分)即可行域。
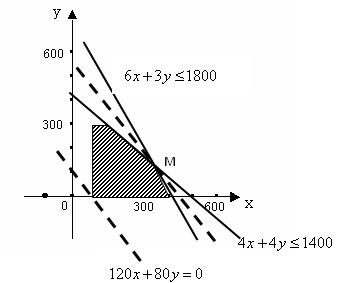
解方程组 得M点的坐标为(250,100) 所以当x =" 250" , y ="100 " 时
得M点的坐标为(250,100) 所以当x =" 250" , y ="100 " 时 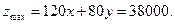 答:该公司每月生产布料A、B分别为250 、100匹时,能够产生最大的利润,最大的利润是38000 元
答:该公司每月生产布料A、B分别为250 、100匹时,能够产生最大的利润,最大的利润是38000 元
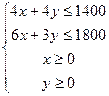 ①; 目标函数为
①; 目标函数为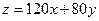 = 40(3 x + 2 y )
= 40(3 x + 2 y ) 作出二元一次不等式① 所表示的平面区域(阴影部分)即可行域。

解方程组
 得M点的坐标为(250,100) 所以当x =" 250" , y ="100 " 时
得M点的坐标为(250,100) 所以当x =" 250" , y ="100 " 时 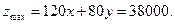 答:该公司每月生产布料A、B分别为250 、100匹时,能够产生最大的利润,最大的利润是38000 元
答:该公司每月生产布料A、B分别为250 、100匹时,能够产生最大的利润,最大的利润是38000 元略

练习册系列答案
相关题目
 ,深为3m,如果池底每平方米造价为80元,池壁每平方米造价为60元,问怎样设计水池能使总造价最低,最低总造价是多少元?
,深为3m,如果池底每平方米造价为80元,池壁每平方米造价为60元,问怎样设计水池能使总造价最低,最低总造价是多少元?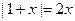 的根.
的根.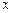 万元,甲、乙两种商品可分别获得
万元,甲、乙两种商品可分别获得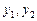 万元的利润,利润曲线
万元的利润,利润曲线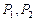 如图,为使投资获得最大利润,应怎样分配投资额,才能获最大利润。
如图,为使投资获得最大利润,应怎样分配投资额,才能获最大利润。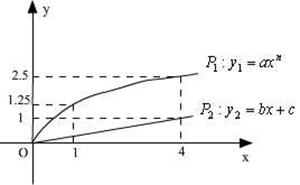
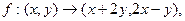 在影射
在影射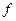 下(3,1)的原象为 ( )
下(3,1)的原象为 ( )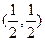
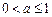 ,函数
,函数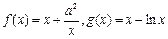 ,若对任意的
,若对任意的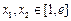 ,都有
,都有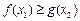 成立,则实数
成立,则实数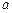 的取值范围为
的取值范围为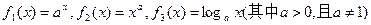 在同一坐标系中画出其中两个函数在第一象限内的图象,其中正确的是( ▲ )
在同一坐标系中画出其中两个函数在第一象限内的图象,其中正确的是( ▲ ) 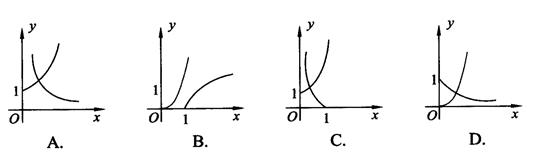
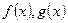 表示相等函数的是( )
表示相等函数的是( )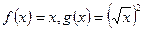 B
B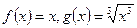
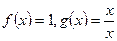 D
D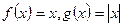
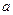 元,每期利率为
元,每期利率为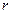 ,存期为
,存期为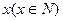 ,则本利和
,则本利和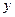 随存期
随存期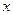 变化的函数解析式为 .
变化的函数解析式为 .