题目内容
3.在△ABC中,角A,B,C所对的边分别是a,b,c,且A,B,C成等差数列,(1)若a=1,b=$\sqrt{3}$,求sinC;
(2)若a,b,c成等差数列,试判断△ABC的形状.
分析 (1)由三角形内角和定理结合A,B,C成等差数列求得B,再由正弦定理求出A,则C可求,答案可求;
(2)由a,b,c成等差数列,可得a,b,c的关系式,再结合余弦定理可得a=c,则可判断△ABC的形状.
解答 解:(1)由A+B+C=π,2B=A+C,得B=$\frac{π}{3}$.
由$\frac{a}{sinA}=\frac{b}{sinB}$,得$\frac{1}{sinA}=\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$,得sinA=$\frac{1}{2}$,
又0<A<B,∴A=$\frac{π}{6}$,则C=$π-\frac{π}{3}-\frac{π}{6}=\frac{π}{2}$.
∴sinC=1;
(2)证明:由2b=a+c,得4b2=a2+2ac+c2,
又b2=a2+c2-ac,
得4a2+4c2-4ac=a2+2ac+c2,
得3(a-c)2=0,∴a=c,
∴A=C,又A+C=$\frac{2π}{3}$,∴A=C=B=$\frac{π}{3}$,
∴△ABC是等边三角形.
点评 本题考查解三角形,关键是对A,B,C成等差数列的应用,是中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
15.已知一个正四面体纸盒的棱长为$2\sqrt{6}$,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )
| A. | 1 | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
13.在映射f:A→B中,A=B={(x,y)|x,y∈R},且f:(x,y)→(2x-y,x+2y),则元素(1,-2)在f的作用下的原像为( )
| A. | (4,-3) | B. | (-$\frac{2}{5}$,-$\frac{8}{5}$) | C. | (-$\frac{2}{5}$,$\frac{1}{5}$) | D. | (0,-1) |
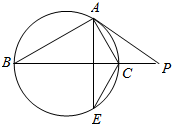 若图中,PA切⊙O于点A,PCB交⊙O于C、B两点,且PCB过点O,AE⊥BP交⊙O于E,则图中与∠CAP相等的角的个数是( )
若图中,PA切⊙O于点A,PCB交⊙O于C、B两点,且PCB过点O,AE⊥BP交⊙O于E,则图中与∠CAP相等的角的个数是( ) 在三棱柱ABC-A1B1C1中,△ABC是边长为2正三角形,D、E分别是线段BB1、AC1的中点,DE⊥AC1.
在三棱柱ABC-A1B1C1中,△ABC是边长为2正三角形,D、E分别是线段BB1、AC1的中点,DE⊥AC1. 如图所示的程序框图,运行相应的程序,若输入x的值为-4,则输出y的值为2.
如图所示的程序框图,运行相应的程序,若输入x的值为-4,则输出y的值为2.