题目内容
5.设数列{an}的前n项和为Sn,且 Sn=n2-4n+4.(1)求数列{an}的通项公式;
(2)设bn=$\frac{a_n}{2^n}$,数列{bn}的前n项和为Tn,求Tn的表达式.
分析 (1)由Sn=n2-4n+4,取n=1得首项,当n≥2时,由an=Sn-Sn-1得数列通项公式;
(2)把数列{an}的通项公式代入bn=$\frac{a_n}{2^n}$,整理后利用错位相减法求数列{bn}的前n项和为Tn.
解答 解:(1)由Sn=n2-4n+4,得${a}_{1}={S}_{1}={1}^{2}-4×1+4=1$,
当n≥2时,an=Sn-Sn-1=n2-4n+4-(n-1)2+4(n-1)-4=2n-5.
当n=1时上式不成立,
${a}_{n}=\left\{\begin{array}{l}{1,n=1}\\{2n-5,n≥2}\end{array}\right.$;
(2)bn=$\frac{a_n}{2^n}$=$\left\{\begin{array}{l}{\frac{1}{2},n=1}\\{\frac{2n-5}{{2}^{n}},n≥2}\end{array}\right.$,
∴Tn=b1+b2+…+bn=$\frac{1}{2}$+Rn,
${R}_{n}=\frac{-1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{2n-5}{{2}^{n}}$,
$\frac{1}{2}{R}_{n}=\frac{-1}{{2}^{3}}+\frac{1}{{2}^{4}}+…+\frac{2n-7}{{2}^{n}}+\frac{2n-5}{{2}^{n+1}}$,
两式作差得:$\frac{1}{2}{R}_{n}=-\frac{1}{4}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n-1}}-\frac{2n-5}{{2}^{n+1}}$
=$\frac{\frac{1}{8}(1-\frac{1}{{2}^{n-3}})}{1-\frac{1}{2}}-\frac{2n-5}{{2}^{n+1}}$=$\frac{1}{4}(1-\frac{1}{{2}^{n-3}})-\frac{2n-5}{{2}^{n+1}}$,
∴${R}_{n}=\frac{1}{2}-\frac{2n+3}{{2}^{n+1}}$,
则${T}_{n}=1-\frac{2n+3}{{2}^{n+1}}$.
点评 本题考查了由数列的前n项和求数列的通项公式,考查了错位相减法求数列的前n项和,是中档题.

| A. | 4024 | B. | 4023 | C. | 2012 | D. | 2015 |
| A. | a|c|<b|c| | B. | ab<bc | C. | a-c<b-c | D. | $\frac{1}{a}>\frac{1}{b}>\frac{1}{c}$ |
| A. | 平行 | B. | 相交 | C. | 异面 | D. | 以上均有可能 |
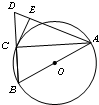 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=8,DC=4,则DE=2.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=8,DC=4,则DE=2.