题目内容
下列结论中正确命题的个数是
①命题p:“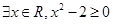 ”的否定形式为
”的否定形式为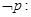 “
“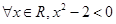 ;
;
② 若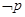 是q的必要条件,则p是
是q的必要条件,则p是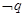 的充分条件;
的充分条件;
③ “M>N”是“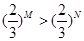 ”的充分不必要条件.
”的充分不必要条件.
①命题p:“
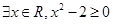 ”的否定形式为
”的否定形式为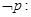 “
“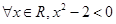 ;
;② 若
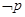 是q的必要条件,则p是
是q的必要条件,则p是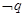 的充分条件;
的充分条件;③ “M>N”是“
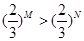 ”的充分不必要条件.
”的充分不必要条件. | A.0 | B.1 | C.2 | D.3 |
C
解:①∵命题“?x∈R,x2-2≥0”是特称命题
∴否定命题为:“?x∈R,x2-2<0,故①正;.
②解:∵¬p是q的必要条件,
∴q?-p为真命题,
故p?-q为真命题
故p是¬q的充分条件,故②正确;
③∵函数y=(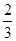 )x在R上单调递减,
)x在R上单调递减,
∴M>N?(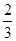 )M<(
)M<(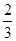 )N,
)N,
因此“M>N”是“(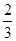 )M>(
)M>(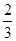 )N”的既不充分也不必要条件,故③错,
)N”的既不充分也不必要条件,故③错,
故选C.
∴否定命题为:“?x∈R,x2-2<0,故①正;.
②解:∵¬p是q的必要条件,
∴q?-p为真命题,
故p?-q为真命题
故p是¬q的充分条件,故②正确;
③∵函数y=(
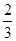 )x在R上单调递减,
)x在R上单调递减,∴M>N?(
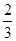 )M<(
)M<(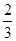 )N,
)N,因此“M>N”是“(
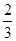 )M>(
)M>(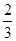 )N”的既不充分也不必要条件,故③错,
)N”的既不充分也不必要条件,故③错,故选C.

练习册系列答案
相关题目
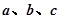 直线,
直线,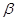 是平面,给出下列命题:(1)若
是平面,给出下列命题:(1)若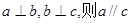 ;②若
;②若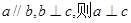 ;③若
;③若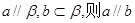 ;④若a与b异面,且
;④若a与b异面,且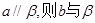 相交;⑤若a与b异面,则至多有一条直线与a,b都垂直.其中真命题的个数是( )
相交;⑤若a与b异面,则至多有一条直线与a,b都垂直.其中真命题的个数是( )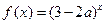 是增函数,若p或q为真,p且q为假,求实数a的取值范围.
是增函数,若p或q为真,p且q为假,求实数a的取值范围.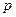
 :
: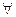
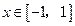 , 不等式
, 不等式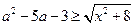 恒成立;命题
恒成立;命题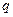 :只有一个实数
:只有一个实数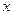 满足不等式
满足不等式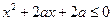 ,若命题“p或q”是真命题,“非q”是真命题,求实数a的取值范围.
,若命题“p或q”是真命题,“非q”是真命题,求实数a的取值范围.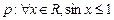 ,则( )
,则( )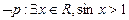
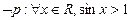
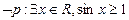
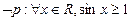
 ①函数
①函数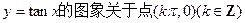 对称;
对称;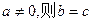 ;
; 的图象;
的图象;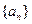 既是等差数列又是等比数列,则
既是等差数列又是等比数列,则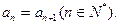
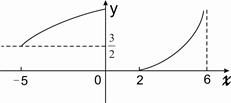
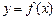 的图象如图所示,命题:
的图象如图所示,命题: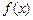 的定义域是[-5,6);
的定义域是[-5,6);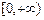 ;
;
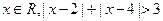 ”的否定是____▲____
”的否定是____▲____