��Ŀ����
����Ŀ��Ϊ�˿���ij��2000�����˵���������������������˸ó�n������ij��IJ�������λ��������������õ����µ�Ƶ�ʷֲ�ֱ��ͼ����Ʒ�����ķ�������Ϊ[10��15����[15��20����[20��25����[25��30����[30��35]�������в�����[20��25���Ĺ�����6����
��������һ�������С��25�Ĺ���������
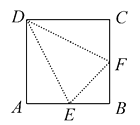
�������涨�Ӳ�������20���Ĺ����������ѡȡ2�����˽�����ѵ������2�����˲���ͬһ��ĸ��ʣ�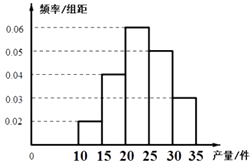
���𰸡��⣺����������ã�����Ϊ[20��25���ĸ���Ϊ0.06��5=0.3
��n= ![]() =20��
=20��
����һ�������С��25�Ĺ�������20��
����һ�������С��25�Ĺ�������Ϊ��0.05+0.03����5��20=8
����������ã�����Ϊ[10��15����������Ϊ20��0.02��5=2��
�����Ƿֱ���A��B��������[15��20����������Ϊ20��0.04��5=4��
�����Ƿֱ�Ϊ�ǣ�a��b��c��d��
��Ӳ�������20���Ĺ�����ѡȡ2�����˵Ľ��Ϊ����A��B������A��a������A��b������A��c����A��d����
��B��a������B��b������B��c����B��d������a��b������a��c������a��d������b��c������b��d������c��d������15�ֽ����
����2�����˲���ͬһ��Ľ��Ϊ
��A��a������A��b������A��c����A��d������B��a������B��b������B��c����B��d������8�֣�
����2�����˲���ͬһ��ĸ���Ϊ�� ![]()
����������1������Ƶ��ֱ��ͼ�ó�����Ϊ[20��25���ĸ���Ϊ0.06��5=0.3�����ݸ��ʿɵõ�����ȡ��20�����˽��е��飬�����õ���һ�������С��25�Ĺ�������8����2������Ƶ��ֱ��ͼ�ɵó�����Ϊ[10��15����������Ϊ2����[15��20����������,4��ʹ���оٷ��õ��Ӳ�������20���Ĺ�����ѡȡ2�����˹���15�ֽ��������2�����˲���ͬһ��Ĺ���8�ֽ�����ʿ����2�����˲���ͬһ��ĸ���.
�����㾫����������Ĺؼ���������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д�