题目内容
(12分)已知过点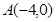 的动直线
的动直线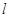 与抛物线
与抛物线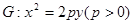 相交于
相交于 两点,当直线
两点,当直线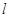 的斜率是
的斜率是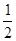 时,
时,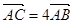 。
。
(1)求抛物线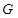 的方程;(5分)
的方程;(5分)
(2)设线段 的中垂线在
的中垂线在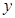 轴上的截距为
轴上的截距为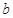 ,求
,求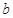 的取值范围。(7分)
的取值范围。(7分)
【答案】
(1)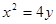 (2)
(2)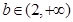
【解析】
试题分析:(1)设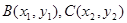 ,当直线
,当直线 的斜率是
的斜率是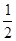 时,
时, 的方程为
的方程为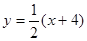 ,
,
即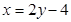 ,由
,由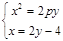 得
得 ,
,
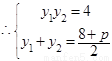 ,又
,又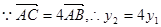 ,由这三个表达式及
,由这三个表达式及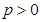 得
得
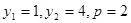 ,则抛物线的方程为
,则抛物线的方程为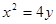
(2)设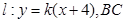 的中点坐标为
的中点坐标为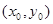
由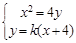 得
得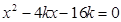
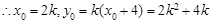 ,
,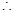 线段
线段 的中垂线方程为
的中垂线方程为
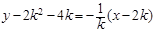 ,
,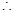 线段
线段 的中垂线在
的中垂线在 轴上的截距为:
轴上的截距为:
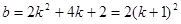 ,由
,由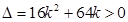 得
得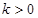 或
或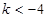
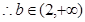
考点:求抛物线方程及直线与抛物线位置关系
点评:本题中向量转化为点的坐标,用纵坐标y值比较简单

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
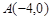 的动直线
的动直线 与抛物线
与抛物线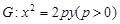 相交于
相交于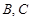 两点,当直线
两点,当直线 时,
时,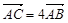
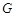 的方程;(2)设线段
的方程;(2)设线段 的中垂线在
的中垂线在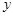 轴上的截距为
轴上的截距为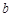 ,求
,求 的动直线
的动直线 与抛物线
与抛物线 相交于
相交于 两点,当直线斜率是
两点,当直线斜率是 时,
时,
 的方程;
的方程; 中垂线在
中垂线在 轴上截距是
轴上截距是 ,求
,求 的动直线
的动直线 与抛物线
与抛物线 相交于
相交于 两点.当直线
两点.当直线 时,
时, .
. 的方程;
的方程; 的中垂线在
的中垂线在 轴上的截距为
轴上的截距为 ,求
,求 ,C
,C ,当直线
,当直线 ,即
,即 (1’)
(1’) 得
得 ,
, (3’)
(3’) ,
, (4’)
(4’) G方程为
G方程为 (5’)
(5’) ,BC中点坐标为
,BC中点坐标为 (6’)
(6’) 得
得 由
由 得
得 (8’)
(8’)

 (10’)
(10’) (11’)
(11’)