题目内容
设函数f(x)=x2-alnx与 的图象分别交直线x=1于点A,B,且曲线y=f(x)在点A处的切线与曲线y=g(x)在点B处的切线平行(斜率相等).
的图象分别交直线x=1于点A,B,且曲线y=f(x)在点A处的切线与曲线y=g(x)在点B处的切线平行(斜率相等).(1)求函数f(x),g(x)的表达式;
(2)当a>1时,求函数h(x)=f(x)-g(x)的最小值;
(3)当a<1时,不等式f(x)≥m•g(x)在
 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.
【答案】分析:(1)求出函数f(x)和g(x)的导函数并求出它们在x=1的导数值,由导数值相等求出a的值则两个函数的解析式可求;
(2)把a=2代入两个函数解析式,求出函数h(x),求导后把导函数进行因式分解,然后由x=1对定义域分段,求出导函数在两段内的符号,判出单调性,从而求得函数h(x)的最小值;
(3)把a= 分别代入函数f(x)和g(x)的解析式,分别求出导函数后判断各自导函数在
分别代入函数f(x)和g(x)的解析式,分别求出导函数后判断各自导函数在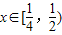 上的符号,由导函数的符号得到原函数的单调性,进一步得到函数f(x)在
上的符号,由导函数的符号得到原函数的单调性,进一步得到函数f(x)在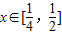 上的最小值和函数g(x)在
上的最小值和函数g(x)在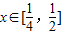 上的最大值,把不等式f(x)≥m•g(x)分离参数m后求出
上的最大值,把不等式f(x)≥m•g(x)分离参数m后求出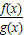 的最小值,则实数m的取值范围可求.
的最小值,则实数m的取值范围可求.
解答:解:(1)由f(x)=x2-alnx,得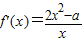 ,所以f′(1)=2-a.
,所以f′(1)=2-a.
由 ,得
,得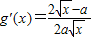 ,所以
,所以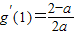 .
.
又由题意可得f'(1)=g'(1),
即 ,故a=2,或
,故a=2,或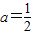 .
.
所以当a=2时,f(x)=x2-2lnx,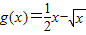 ;
;
当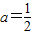 时,
时,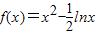 ,
,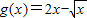 .
.
(2)当a>1时,a=2, ,
,
函数h(x)的定义域为(0,+∞).
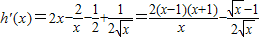
=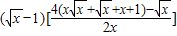 .
.
由x>0,得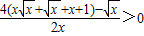 ,
,
故当x∈(0,1)时,h'(x)<0,h(x)递减,
当x∈(1,+∞)时,h'(x)>0,h(x)递增,
所以函数h(x)在(0,+∞)上的最小值为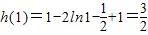 .
.
(3)因为a<1,所以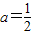 ,此时
,此时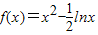 ,
,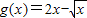 ,
,
当 时,由
时,由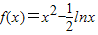 ,得
,得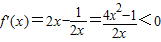 ,
,
f(x)在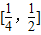 上为减函数,
上为减函数,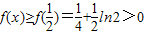 .
.
当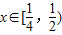 时,由
时,由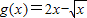 ,得
,得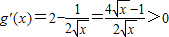 ,
,
g(x)在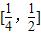 上为增函数,
上为增函数,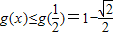 ,且
,且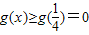 .
.
要使不等式f(x)≥m•g(x)在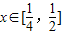 上恒成立,当
上恒成立,当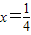 时,m为任意实数;
时,m为任意实数;
当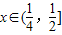 时,不等式f(x)≥m•g(x)化为
时,不等式f(x)≥m•g(x)化为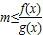 ,
,
而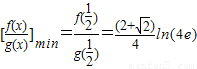 .
.
所以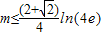 .
.
所以当a<1时,不等式f(x)≥m•g(x)在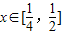 上恒成立的实数m的取值范围为
上恒成立的实数m的取值范围为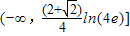 .
.
点评:本题考查了利用导数研究曲线上某点的切线方程,考查了利用导数求闭区间上函数的最值,训练了利用分离变量求参数的取值范围,考查了学生的运算能力,在分类讨论时,此题对细节的分类要求较高,属难度较大的题目.
(2)把a=2代入两个函数解析式,求出函数h(x),求导后把导函数进行因式分解,然后由x=1对定义域分段,求出导函数在两段内的符号,判出单调性,从而求得函数h(x)的最小值;
(3)把a=
 分别代入函数f(x)和g(x)的解析式,分别求出导函数后判断各自导函数在
分别代入函数f(x)和g(x)的解析式,分别求出导函数后判断各自导函数在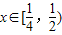 上的符号,由导函数的符号得到原函数的单调性,进一步得到函数f(x)在
上的符号,由导函数的符号得到原函数的单调性,进一步得到函数f(x)在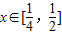 上的最小值和函数g(x)在
上的最小值和函数g(x)在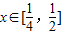 上的最大值,把不等式f(x)≥m•g(x)分离参数m后求出
上的最大值,把不等式f(x)≥m•g(x)分离参数m后求出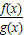 的最小值,则实数m的取值范围可求.
的最小值,则实数m的取值范围可求.解答:解:(1)由f(x)=x2-alnx,得
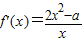 ,所以f′(1)=2-a.
,所以f′(1)=2-a.由
 ,得
,得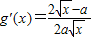 ,所以
,所以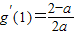 .
.又由题意可得f'(1)=g'(1),
即
 ,故a=2,或
,故a=2,或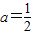 .
.所以当a=2时,f(x)=x2-2lnx,
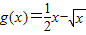 ;
;当
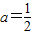 时,
时,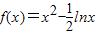 ,
,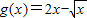 .
.(2)当a>1时,a=2,
 ,
,函数h(x)的定义域为(0,+∞).
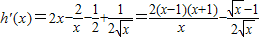
=
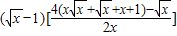 .
.由x>0,得
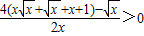 ,
,故当x∈(0,1)时,h'(x)<0,h(x)递减,
当x∈(1,+∞)时,h'(x)>0,h(x)递增,
所以函数h(x)在(0,+∞)上的最小值为
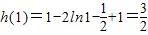 .
.(3)因为a<1,所以
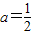 ,此时
,此时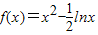 ,
,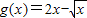 ,
,当
 时,由
时,由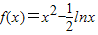 ,得
,得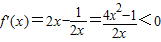 ,
,f(x)在
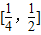 上为减函数,
上为减函数,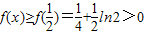 .
.当
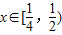 时,由
时,由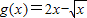 ,得
,得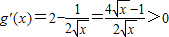 ,
,g(x)在
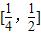 上为增函数,
上为增函数,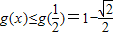 ,且
,且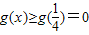 .
.要使不等式f(x)≥m•g(x)在
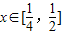 上恒成立,当
上恒成立,当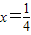 时,m为任意实数;
时,m为任意实数;当
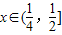 时,不等式f(x)≥m•g(x)化为
时,不等式f(x)≥m•g(x)化为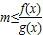 ,
,而
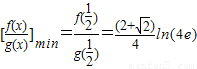 .
.所以
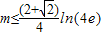 .
.所以当a<1时,不等式f(x)≥m•g(x)在
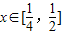 上恒成立的实数m的取值范围为
上恒成立的实数m的取值范围为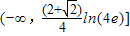 .
.点评:本题考查了利用导数研究曲线上某点的切线方程,考查了利用导数求闭区间上函数的最值,训练了利用分离变量求参数的取值范围,考查了学生的运算能力,在分类讨论时,此题对细节的分类要求较高,属难度较大的题目.

练习册系列答案
相关题目