题目内容
(本小题满分12分)
已知函数f(x)=x3-ax2,其中a为实常数.
(1)设当x∈(0,1)时,函数y = f(x)图象上任一点P处的切线的斜线率为k,若k≥-1,求a的取值范围
(2)当x∈[-1,1]时,求函数y=f(x)+a(x2-3x)的最大值.
(1) (-∞,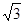 ].
].
(2) g(x)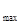
【解析】解:(1)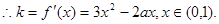
由k≥-1,得3x2-2ax+1≥0,即a≤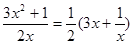 恒成立
恒成立
∴a≤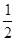 (3x+
(3x+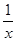 )min
)min
∵当x∈(0,1)时,3x+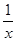 ≥2
≥2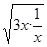 =2
=2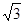 ,当且仅当x=
,当且仅当x=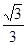 时取等号.
时取等号.
∴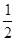 (3x+
(3x+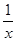 )min =
)min =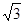 .故a的取值范围是(-∞,
.故a的取值范围是(-∞,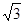 ].
].
(2)设g(x)=f(x)+a(x2-3x)=x3-3ax,x∈[-1,1]则
g′(x)=3x2-3a=3(x2-a).
①当a≥1时,∴g′(x)≤0.从而g(x)在[-1,1]上是减函数.
∴g(x)的最大值为g(-1)=3a-1.
②当0<a<1时,g′(x)=3(x+ )(x-
)(x- ).
).
由g′(x) >0得,x> 或x<-
或x<- :由g′(x)<
0得,-
:由g′(x)<
0得,- <x<
<x< .
.
∴g(x)在[-1,- ],[
],[ ,1]上增函数,在[-
,1]上增函数,在[- ,
, ]上减函数.
]上减函数.
∴g(x)的极大值为g(- )=2a
)=2a .
.
由g(- )-g(1)=2a
)-g(1)=2a +3a-1=(
+3a-1=( +1)
+1)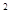 ·(2
·(2 -1)知
-1)知
当2 -1<0,即0≤a<
-1<0,即0≤a<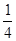 时,g(-
时,g(- )<g(1)
)<g(1)
∴g(x)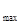 =g(1)=1-3a.
=g(1)=1-3a.
当2 -1≥0,即
-1≥0,即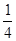 <a<1时,g(-
<a<1时,g(- )≥g(1)
)≥g(1)
∴g(x)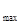 =g(-
=g(- )=2a
)=2a .
.
③当a≤0时,g′(x)≥0,从而g(x)在[-1,1]上是增函数.
∴g(x)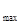 =g(1)=1-3a
=g(1)=1-3a
综上分析,g(x)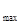
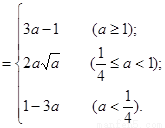

 阅读快车系列答案
阅读快车系列答案