题目内容

（2011•江西模拟）已知函数f(x)=
ex，x≥0
-2x，x＜0
则关于x的方程f[f（x）]+k=0，给出下列四个命题：①存在实数k，使得方程恰有1个不同实根；②存在实数k，使得方程恰有2个不同实根；③存在实数k，使得方程恰有3个不同实根；④存在实数k，使得方程恰有4个不同实根；其中假命题的个数是（　　）
分析：由题意求出函数f[f（x）]的表达式，画出它的图象，利用单调性，判断方程零点的个数即可．
解答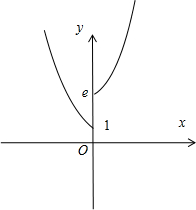：解：因为f(x)=
ex，x≥0
-2x，x＜0
，所以f[f（x）]=
eex≥e ，x≥0
e-2x＞1，x＜0
，
关于x的方程f[f（x）]+k=0，令g（x）=
eex+k，x≥0
e-2x+k，x＜0
，
f[f（x）]的图象大致如图：x＜0是减函数，x≥0是增函数．
方程f[f（x）]+k=0，：①存在实数k，使得方程恰有1个不同实根；正确．
②存在实数k，使得方程恰有2个不同实根；正确．
③存在实数k，使得方程恰有3个不同实根；不正确．
④存在实数k，使得方程恰有4个不同实根；不正确．
正确结果只有①②．
故选C．
点评：本题考查函数的零点与方程的根的问题，求出函数的表达式画出图象是解题的关键．
练习册系列答案
相关题目
（2011•江西模拟）在△ABC中，内角A，B，C的对边分别是a，b，c，若a2-b2=
3
bc，sinC=2
3
sinB，则A=（　　）
（2011•江西模拟）已知数列{an}，{bn}分别是等差、等比数列，且a1=b1=1，a2=b2，a4=b3≠b4．
①求数列{an}，{bn}的通项公式；
②设Sn为数列{an}的前n项和，求{
1
Sn
}的前n项和Tn；
③设Cn=
anbn
Sn+1
（n∈N），Rn=C1+C2+…+Cn，求Rn．
（2011•江西模拟）已知数列{an}满足an+1=
2an
an+2
（n∈N*），a2011=
1
2011
．
（1）求{an}的通项公式；
（2）若bn=
4
an
-4023且cn=
b
2
n+1
+
b
2
n
2bn+1bn
(n∈N*)，求证：c1+c2+…+cn＜n+1．
（2011•江西模拟）已知函数f（x）=ax-lnx+1（a∈R），g（x）=xe1-x．
（1）求函数g（x）在区间（0，e]上的值域；
（2）是否存在实数a，对任意给定的x0∈（0，e]，在区间[1，e]上都存在两个不同的xi（i=1，2），使得f（xi）=g（x0）成立．若存在，求出a的取值范围；若不存在，请说明理由．
（3）给出如下定义：对于函数y=F（x）图象上任意不同的两点A（x1，y1），B（x2，y2），如果对于函数y=F（x）图象上的点M（x0，y0）（其中x0=
x1+x22
)总能使得F（x1）-F（x2）=F'（x0）（x1-x2）成立，则称函数具备性质“L”，试判断函数f（x）是不是具备性质“L”，并说明理由．
（2011•江西模拟）设a∈R，f(x)=cosx(asinx-cosx)+cos2(
π
2
-x)满足f(-
π
3
)=f(0)，
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）设△ABC三内角A，B，C所对边分别为a，b，c且
a2+c2-b2
a2+b2-c2
=
c
2a-c
，求f（x）在（0，B]上的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网