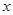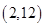Question

（本小题满分12分）

某商品每件成本9元，售价为30元，每星期卖出432件，如果降低价格，销售量可以增加，且每星期多卖出商品件数与商品单价的降低值x(单位：元，0≤x≤30)的平方成正比，已知商品单价降低2元时，一星期多卖出24件

（1）将一个星期的商品销售利润表示成x的函数；

（2）如何定价才能使一个星期的商品销售利润最大？

 

Answer 1

【答案】

（1）

（2）定价为18元时利润最大。

【解析】解:（1）设商品降价x元，则多卖出的商品数为kx²,在一个星期内商品的销售利润为   由题意得:24=k·2²,  ∴k=6,              …………………………2分

所以

                                          …………………………6分

⑵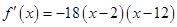               …………………………8分

令得x=2或x=12,

		2		12
	—	0	+	0	—
	单调递减	极小值	单调递增	极大值	单调递减

由上表可知当x=12时，取得极大值，而>

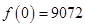
∴定价为18元时利润最大                      …………………………12分