题目内容
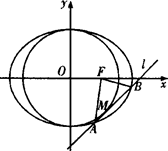
如图,在平面直角坐标系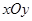 中,
中, 、
、 分别是椭圆
分别是椭圆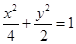 的顶点,过坐标原点的直线交椭圆于
的顶点,过坐标原点的直线交椭圆于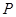 、
、 两点,其中
两点,其中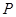 在第一象限.过
在第一象限.过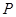 作
作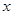 轴的垂线,垂足为
轴的垂线,垂足为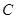 .连接
.连接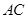 ,并延长交椭圆于点
,并延长交椭圆于点 .设直线
.设直线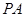 的斜率为
的斜率为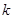 .
.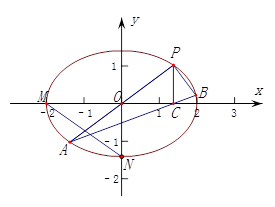
(Ⅰ)当直线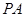 平分线段
平分线段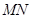 时,求
时,求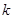 的值;
的值;
(Ⅱ)当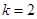 时,求点
时,求点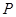 到直线
到直线 的距离;
的距离;
(Ⅲ)对任意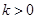 ,求证:
,求证: .
.
(Ⅰ)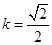 ;(Ⅱ)
;(Ⅱ)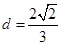 ;(Ⅲ)详见解析
;(Ⅲ)详见解析
解析试题分析:(Ⅰ)求出点 、
、 的中点坐标,再用斜率公式可求得
的中点坐标,再用斜率公式可求得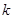 的值;(Ⅱ)求出直线
的值;(Ⅱ)求出直线 的方程,再用点到直线的距离公式可求得点
的方程,再用点到直线的距离公式可求得点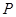 到直线
到直线 的距离;
的距离;
(Ⅲ)思路一:圆锥曲线题型的一个基本处理方法是设而不求,其核心是利用 ----(*).要证明
----(*).要证明 ,只需证明它们的斜率之积为-1. 但直接求它们的积,不好用(*)式,此时需要考虑转化.
,只需证明它们的斜率之积为-1. 但直接求它们的积,不好用(*)式,此时需要考虑转化.
思路二:设 ,然后用
,然后用 表示出
表示出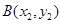 的坐标.这种方法要注意直线
的坐标.这种方法要注意直线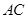 的方程应设为:
的方程应设为:  ,若用点斜式,则运算量大为增加.
,若用点斜式,则运算量大为增加.
此类题极易在运算上出错,需倍加小心.
试题解析:(Ⅰ)由题设知:  ,所以线段
,所以线段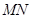 的中点为
的中点为 ,
,
由于直线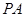 平分线段
平分线段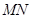 ,故直线
,故直线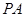 过线段
过线段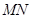 的中点,又直线
的中点,又直线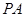 过坐标原点,
过坐标原点,
所以
(Ⅱ)将直线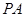 的方程
的方程 代入椭圆方程
代入椭圆方程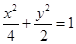 得:
得:  ,因此
,因此
于是 ,由此得直线
,由此得直线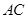 的方程为:
的方程为: 
所以点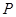 到直线
到直线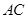 即
即 的距离
的距离
(Ⅲ)法一:设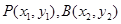 ,则
,则
由题意得: 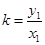
设直线 的斜率分别为
的斜率分别为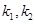 ,因为
,因为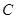 在直线
在直线 上,所以
上,所以
从而 ,所以:
,所以:
法二: 
所以直线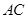 的方程为:
的方程为:  代入椭圆方程
代入椭圆方程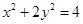 得:
得:
由韦达定理得: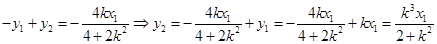
所以
 ,
,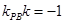 所以
所以
考点:本题考查椭圆的方程、直线的方程,中点坐标公式,点到直线的距离,两直线垂直的判定;考查韦达定理.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
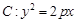 的焦点坐标为
的焦点坐标为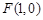 ,过
,过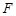 的直线交抛物线
的直线交抛物线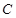 于
于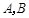 两点,直线
两点,直线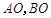 分别与直线
分别与直线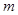 :
: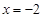 相交于
相交于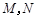 两点.
两点.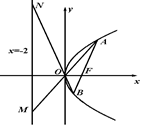
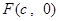 是椭圆
是椭圆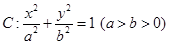 的右焦点,圆
的右焦点,圆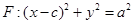 与
与 轴交于
轴交于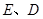 两点,
两点,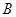 是椭圆
是椭圆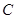 与圆
与圆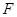 的一个交点,且
的一个交点,且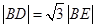
 与
与 ,且
,且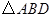 的面积为
的面积为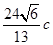 ,求椭圆
,求椭圆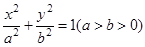 的离心率为
的离心率为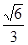 ,且过点
,且过点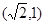 .
.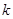 的直线
的直线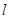 与椭圆相交于不同的两点
与椭圆相交于不同的两点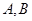 ,试问在
,试问在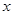 轴上是否存在点
轴上是否存在点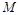 ,使
,使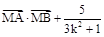 是与
是与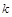 无关的常数?若存在,求出点
无关的常数?若存在,求出点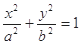 (
(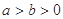 )右顶点到右焦点的距离为
)右顶点到右焦点的距离为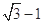 ,短轴长为
,短轴长为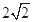 .
.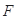 的直线与椭圆分别交于
的直线与椭圆分别交于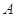 、
、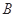 两点,若线段
两点,若线段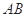 的长为
的长为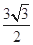 ,求直线
,求直线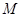 是椭圆
是椭圆 :
: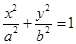
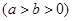 上一点,
上一点, 分别为
分别为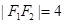 ,
,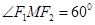 ,
,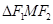 的面积为
的面积为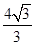 .
.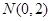 ,过点
,过点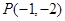 作直线
作直线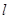 ,交椭圆
,交椭圆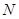 的
的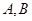 两点,直线
两点,直线 的斜率分别为
的斜率分别为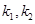 ,证明:
,证明: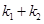 为定值.
为定值.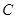 的中心在坐标原点,右准线为
的中心在坐标原点,右准线为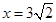 ,离心率为
,离心率为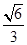 .若直线
.若直线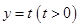 与椭圆
与椭圆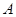 、
、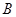 ,以线段
,以线段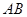 为直径作圆
为直径作圆 .
.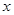 轴相切,求圆
轴相切,求圆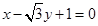 截得的线段长.
截得的线段长.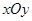 中,已知曲线
中,已知曲线 上任意一点到点
上任意一点到点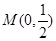 的距离与到直线
的距离与到直线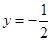 的距离相等.
的距离相等.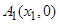 ,
,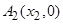 是
是 轴上的两点
轴上的两点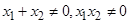 ,过点
,过点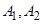 分别作
分别作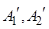 ,直线
,直线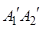 与x轴交于点
与x轴交于点 ,这样就称
,这样就称 确定了
确定了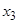 .同样,可由
.同样,可由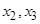 确定了
确定了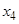 .现已知
.现已知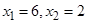 ,求
,求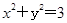 的半径等于椭圆E:
的半径等于椭圆E: (a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x-
(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x- 的距离为
的距离为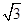 -
-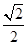 ,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).