题目内容
(10分)设函数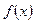 的定义域是
的定义域是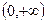 ,且对任意的正实数
,且对任意的正实数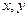 都有
都有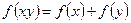 恒成立. 已知
恒成立. 已知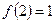 ,且
,且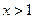 时,
时,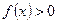 .
.
(1)求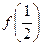 的值K]
的值K]
(2)判断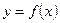 在
在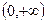 上的单调性,并给出你的证明
上的单调性,并给出你的证明
(3)解不等式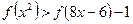 .
.
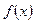 的定义域是
的定义域是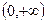 ,且对任意的正实数
,且对任意的正实数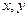 都有
都有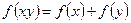 恒成立. 已知
恒成立. 已知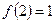 ,且
,且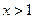 时,
时,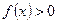 .
.(1)求
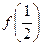 的值K]
的值K](2)判断
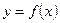 在
在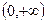 上的单调性,并给出你的证明
上的单调性,并给出你的证明(3)解不等式
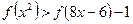 .
.解:(1)令x=y="1," 则可得f(1)="0," 再令x="2," y=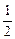 , 得f(1)=f(2)+f(
, 得f(1)=f(2)+f(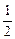 ), 故f(
), 故f(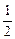 )= -1………2分
)= -1………2分
 (2)设0<x1<x2, 则f(x1) +f(
(2)设0<x1<x2, 则f(x1) +f(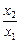 )=f(x2) 即f(x2) -f(x1)=f(
)=f(x2) 即f(x2) -f(x1)=f(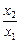 ),
),
∵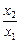 >1, 故f(
>1, 故f(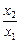 )>0, 即f(x2)>f(x1) 故f(x)在(0, +∞)上为增函数……………………6分
)>0, 即f(x2)>f(x1) 故f(x)在(0, +∞)上为增函数……………………6分
(3)由f(x2)>f(8x-6) -1得f(x2)>f(8x-6) +f(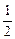 )=f [
)=f [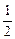 (8x-6)],
(8x-6)],
故得x2>4x-3且8x-6>0, 解得解集为{x|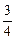 <x<1或x>3}………………………10分
<x<1或x>3}………………………10分
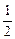 , 得f(1)=f(2)+f(
, 得f(1)=f(2)+f(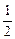 ), 故f(
), 故f(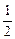 )= -1………2分
)= -1………2分 (2)设0<x1<x2, 则f(x1) +f(
(2)设0<x1<x2, 则f(x1) +f(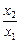 )=f(x2) 即f(x2) -f(x1)=f(
)=f(x2) 即f(x2) -f(x1)=f(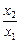 ),
), ∵
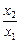 >1, 故f(
>1, 故f(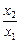 )>0, 即f(x2)>f(x1) 故f(x)在(0, +∞)上为增函数……………………6分
)>0, 即f(x2)>f(x1) 故f(x)在(0, +∞)上为增函数……………………6分(3)由f(x2)>f(8x-6) -1得f(x2)>f(8x-6) +f(
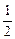 )=f [
)=f [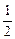 (8x-6)],
(8x-6)], 故得x2>4x-3且8x-6>0, 解得解集为{x|
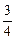 <x<1或x>3}………………………10分
<x<1或x>3}………………………10分略

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
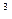 +3x
+3x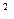 +ax+b)e
+ax+b)e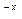 。
。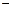 3 ,求f (x) 的单调区间;
3 ,求f (x) 的单调区间;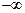 ,
,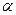 ),(2,
),(2,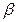 )上单调递增,在(
)上单调递增,在(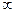 )上单调递减,证明:
)上单调递减,证明: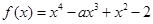 有且仅有一个极值点,则实数
有且仅有一个极值点,则实数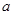 的取值范围 ( )
的取值范围 ( ) ,
, 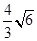 ]
]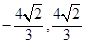 ]
]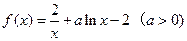 .
.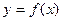 在点
在点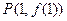 处的切线与直线
处的切线与直线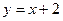 垂直,求函数
垂直,求函数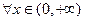 都有
都有 成立,试求
成立,试求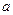 的取值范围;
的取值范围;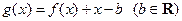 .当
.当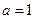 时,函数
时,函数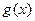 在区间
在区间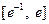 上有两个零点,
上有两个零点, .
.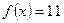 时,求
时,求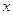 的值;
的值;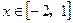 时,求
时,求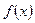 的最大值和最小值。
的最大值和最小值。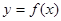 的导函数
的导函数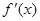 的图象,则下面判断正确的是( )
的图象,则下面判断正确的是( )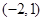 上
上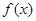 是增函数
是增函数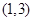 上
上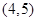 上
上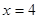 时,
时,
 数
数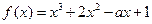 .
.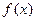 在点
在点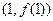 处的切线斜率为4,求实
处的切线斜率为4,求实 数
数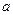 的值;
的值;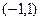 上是单调函数,求实数
上是单调函数,求实数 在
在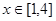 上单调递减,则实数
上单调递减,则实数 的最小值为 ( )
的最小值为 ( )