题目内容
在 中,
中, ,
, ,
, 分别为
分别为 、
、 、
、 的对边,如果
的对边,如果 ,
, ,
, 成等差数列,
成等差数列, ,
, 的面积为
的面积为 ,那么
,那么 ( )
( )
A. | B. | C. | D. |
B
解析试题分析:∵a,b,c成等差数列,∴2b=a+c.
平方得a2+c2=4b2-2ac.
又△ABC的面积为 ,且∠B=30°,
,且∠B=30°,
故由S△=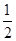 acsinB=
acsinB=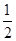 ac•sin30°=
ac•sin30°=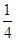 ac=
ac= ,
,
得ac=6,∴a2+c2=4b2-12.
由余弦定理
cosB=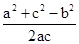 =
=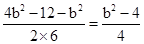 =
=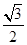 ,
,
解得b2=4+2 .又∵b为边长,∴b=1+
.又∵b为边长,∴b=1+ .选B。
.选B。
考点:等差数列,三角形面积,余弦定理的应用。
点评:中档题,本题综合性较强,综合考查等差数列,三角形面积,余弦定理的应用。通过构建方程组,得到解题目的。

练习册系列答案
相关题目
在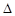 ABC中,A,B,C的对边分别为
ABC中,A,B,C的对边分别为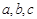 ,且
,且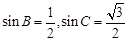 则
则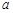 :
: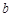 :
: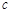 为( )
为( )
A.1: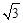 :2 :2 | B.1:1: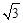 |
C.2:1: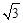 | D.2:1: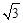 或1:1: 或1:1: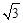 |
在△ABC中,若a = 2 ,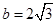 ,
,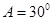 , 则B= ( )
, 则B= ( )
A.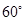 | B.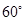 或 或 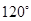 | C.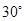 | D.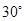 或 或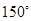 |
在 ABC中,
ABC中, 分别为
分别为 的对边,
的对边, 上的高为
上的高为 ,且
,且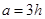 ,则
,则 的最大值为 ( )
的最大值为 ( )
| A.3 | B. | C.2 | D. |
若 中
中 ,
, ,则
,则 =( )
=( )
A. | B. | C. | D. |
在△ABC中,内角A,B,C的对边分别是a,b,c,若 且
且 ,则△ABC的面积为( )
,则△ABC的面积为( )
A. | B. | C. | D. |
在△ABC中,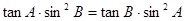 ,那么△ABC一定是( )
,那么△ABC一定是( )
| A.锐角三角形 | B.直角三角形 |
| C.等腰三角形 | D.等腰三角形或直角三角形 |
在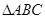 中,角
中,角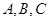 所对边长分别为
所对边长分别为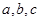 ,若
,若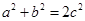 ,则角
,则角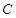 的最大值为( )
的最大值为( )
A.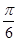 | B.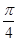 | C.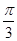 | D.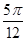 |
在 中,
中,  则
则 等于( )
等于( )
A. | B. | C. | D. |