题目内容
在 ABC中,
ABC中, 分别为
分别为 的对边,
的对边, 上的高为
上的高为 ,且
,且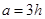 ,则
,则 的最大值为 ( )
的最大值为 ( )
| A.3 | B. | C.2 | D. |
B
解析试题分析:根据题意,由于 ∴由余弦定理c2+b2=a2+2bccosA,
∴由余弦定理c2+b2=a2+2bccosA, ==3sinA+2cosA=
==3sinA+2cosA= sin(A+θ)(tanθ=
sin(A+θ)(tanθ= ).故可知
).故可知 的最大值为
的最大值为 ,选B.
,选B.
考点:余弦定理,三角函数
点评:本题考查三角函数的最值,难点在于三角形的面积公式与余弦定理的综合运用,辅助角公式的使用,属于难题

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
已知 外接圆
外接圆 的半径为
的半径为 ,且
,且 .
. ,从圆
,从圆 内随机取一个点
内随机取一个点 ,若点
,若点 取自内的概率恰为
取自内的概率恰为 ,判断
,判断 的形状.( )
的形状.( )
| A.直角三角形 | B.等边三角形 | C.钝角三角形 | D.等腰直角三角形 |
在△ABC中,若 ,则其面积等于( )
,则其面积等于( )
| A.12 | B.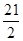 | C.28 | D. |
在 中,若
中,若 ,则B的值为 ( )
,则B的值为 ( )
| A.300 | B.900 | C.600 | D.450 |
已知△ABC满足 , 则角C的大小为( )
, 则角C的大小为( )
A. | B. | C. | D. |
在 中
中 ,
,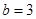 ,
, ,则
,则 =( )
=( )
A. | B.7 | C. | D.13 |
在 中,
中, ,
, ,
, 分别为
分别为 、
、 、
、 的对边,如果
的对边,如果 ,
, ,
, 成等差数列,
成等差数列, ,
, 的面积为
的面积为 ,那么
,那么 ( )
( )
A. | B. | C. | D. |
在△ABC中,其中有两解的是( )
| A.a=8,b=16,A=30° | B.a=30,b=25,A=150° |
| C.a=72,b=50,A=135° | D.a=18,b=20,A=60° |
一个三角形的三边长依次是4、6、 ,这个三角形的面积等于( )
,这个三角形的面积等于( )
A.3 | B.6 | C.3 | D. |