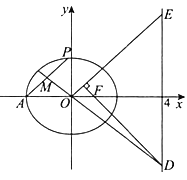
题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,以上顶点和右焦点为直径端点的圆与直线
,以上顶点和右焦点为直径端点的圆与直线![]() 相切.
相切.
(1)求椭圆的标准方程;
(2)对于直线![]() 和点
和点![]() ,椭圆
,椭圆![]() 上是否存在不同的两点
上是否存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,若存在实数
,若存在实数![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)存在,
;(Ⅱ)存在, ![]() .
.
【解析】试题分析:(Ⅰ)由![]() 得
得![]() ,圆的方程为
,圆的方程为![]() ,由圆心到直线的距离等于半径可得
,由圆心到直线的距离等于半径可得![]() ,故可得椭圆方程;(Ⅱ) 设
,故可得椭圆方程;(Ⅱ) 设![]() ,
, ![]() ,直线
,直线![]() 方程为:
方程为: ![]() ,联立方程组结合韦达定理,
,联立方程组结合韦达定理, ![]() ,
, ![]() ,
, ![]() ,结合点
,结合点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上得
上得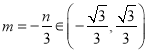 ,由
,由![]() 得
得![]() 的值为
的值为![]() .
.
试题解析:(Ⅰ)由椭圆的离心率![]() 得
得![]() ,得
,得![]() ………………1分
………………1分
上顶点为![]() ,右焦点为
,右焦点为![]() ,
,
以上顶点和右焦点为直径端点的圆的方程为![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,………………3分
,………………3分
椭圆的标准方程为![]() ………………4分
………………4分
(Ⅱ)由题意设![]() ,
, ![]() ,直线
,直线![]() 方程为:
方程为: ![]() .
.
联立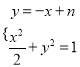 消
消![]() 整理可得:
整理可得: ![]() ,………………5分
,………………5分
由![]() ,解得
,解得![]() ………………6分
………………6分
![]() ,
, ![]() ,
,
设直线![]() 之中点为
之中点为![]() ,则
,则![]() ,………………7分
,………………7分
由点![]() 在直线
在直线![]() 上得:
上得: ![]() ,
,
又点![]() 在直线
在直线![]() 上,
上, ![]() ,所以
,所以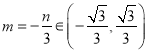 ……①………………9分
……①………………9分
又![]() ,
, ![]() ,
, ![]()
![]()
解得: ![]() 或
或![]() ……②………………11分
……②………………11分
综合①②,![]() 的值为
的值为![]() .………………12分
.………………12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】2017年“一带一路”国际合作高峰论坛于今年5月14日至15日在北京举行.为高标准完成高峰论坛会议期间的志愿服务工作,将从27所北京高校招募大学生志愿者,某调查机构从是否有意愿做志愿者在某高校访问了80人,经过统计,得到如下丢失数据的列联表:(![]() ,表示丢失的数据)
,表示丢失的数据)
无意愿 | 有意愿 | 总计 | |
男 |
|
| 40 |
女 | 5 |
|
|
总计 | 25 |
| 80 |
(1)求出![]() 的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
(2)若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
附参考公式及数据: 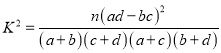 ,其中
,其中![]() .
.
| 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
【题目】某市英才中学的一个社会实践调查小组,在对中学生的良好“光盘习惯”的调查中,随机发放了120份问卷,对收回的120份有效问卷进行统计,得到如下![]() 列联表:
列联表:
做不到光盘 | 能做到光盘 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现已按是否能做到光盘分层从45份女生问卷中抽取9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的份数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过![]() ,那么根据临界值表最精确的
,那么根据临界值表最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量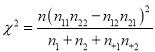 ,其中
,其中![]() .
.
独立性检验临界表:
|
|
|
|
|
|
|
|
|
|
|
|
【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
| 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
(Ⅰ)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;
题号 | 1 | 2 | 3 | 4 | 5 |
实测答对人数 | |||||
实测难度 |
(Ⅱ)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(Ⅲ)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度
题的预估难度![]() .规定:若
.规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.