题目内容
(本小题满分12分〉
在平面直角坐标系xOy中,点P(x,y)为动点,已知点![]() I,直线PA与PB的斜率之积为定值
I,直线PA与PB的斜率之积为定值![]() .
.
(I) 求动点P的轨迹E的方程;
(II)若F(1,0),过点F的直线l交轨迹E于M、N两点,以MN为对角线的正方形的第三个顶点恰在y轴上,求直线l的方程.
解:⑴由题意![]() ,----------- 2分
,----------- 2分
整理得![]() , 所以所求轨迹
, 所以所求轨迹![]() 的方程为
的方程为![]() ,------ 4分
,------ 4分
⑵当直线![]() 与
与![]() 轴重合时,与轨迹
轴重合时,与轨迹![]() 无交点,不合题意;
无交点,不合题意;
当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() ,此时
,此时![]() ,以
,以![]() 为对角线的正方形的另外两个顶点坐标为
为对角线的正方形的另外两个顶点坐标为![]() ,不合题意;--------------- 6分
,不合题意;--------------- 6分
当直线![]() 与
与![]() 轴既不重合,也不垂直时,不妨设直线
轴既不重合,也不垂直时,不妨设直线![]() ,
,
![]() 的中点
的中点![]() ,
,
由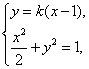 消
消![]() 得
得![]() ,
,
由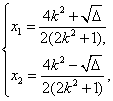 得
得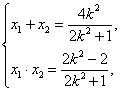 -------------------8分
-------------------8分
所以![]() ,
,
则线段![]() 的中垂线
的中垂线![]() 的方程为:
的方程为:![]()
整理得直线![]() ,
,
则直线![]() 与
与![]() 轴的交点
轴的交点![]() ,
,
注意到以![]() 为对角线的正方形的第三个顶点恰在
为对角线的正方形的第三个顶点恰在![]() 轴上,
轴上,
当且仅当![]() ,
,
即![]() ,----------------10分
,----------------10分
![]() , ①
, ①
由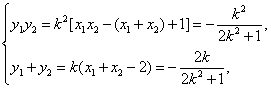 ②
②
将②代入①解得 ![]() ,即直线
,即直线![]() 的方程为
的方程为![]() ,
,
综上,所求直线![]() 的方程为
的方程为![]() 或
或![]() .------------12分
.------------12分
选做题

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目