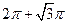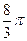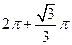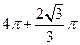题目内容
已知球O是棱长为1的正方体ABCD—A1B1C1D1的内切球，则平面ACD1截球O所得的截面面积为
A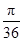． | B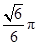． | C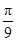． | D． |
A
考点：
分析：根据正方体和球的结构特征，判断出平面ACD1是正三角形，求出它的边长，再通过图求出它的内切圆的半径，最后求出内切圆的面积
解：根据题意知，平面ACD1是边长为
的正三角形，且球与包含上三角形的三边的平面的切点恰好在此三线段的中点，故所求截面的面积是该正三角形的内切圆的面积，则由图得，△ACD1内切圆的半径是 
×tan30°=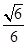
，
则所求的截面圆的面积是π××=．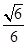
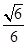故选A．
分析：根据正方体和球的结构特征，判断出平面ACD1是正三角形，求出它的边长，再通过图求出它的内切圆的半径，最后求出内切圆的面积
解：根据题意知，平面ACD1是边长为
的正三角形，且球与包含上三角形的三边的平面的切点恰好在此三线段的中点，故所求截面的面积是该正三角形的内切圆的面积，则由图得，△ACD1内切圆的半径是 ×tan30°=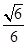，则所求的截面圆的面积是π×
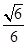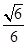×=．故选A．
练习册系列答案
相关题目
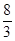
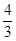
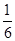B.
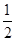
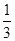D.1
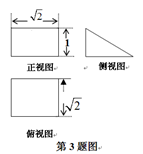
求这两个平行平面的距离．
中，侧棱
、
、
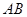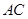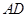两两垂直，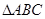
、
、
的面积分别为
、
、
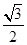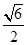，则三棱锥
