题目内容

已知双曲线，点在曲线上，曲线的离心率为，点、为曲线上易于点A的任意两点,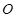为坐标原点。

（1）求曲线上方程；

（2）若为曲线的焦点，求最大值；

（3）若以为直径的圆过点，求证：直线过定点，并求出定点坐标。

 

 

【答案】

（1）方程为

（2）由双曲线的对称性知，不妨设P在左支上，设，由焦半径得：

  ，所以

所以，当时取等号。

的最大值是。

（3）设，联立直线PQ和双曲线方程得：

，所以得。

且，由题知，

所以，

，

代入的，

解得或（舍去），所以PQ方程为，

即得PQ过定点

（说明：另解一，可以利用对称和当PQ垂直情况猜过轴上点，然后证明；

另解二，设AP斜率，求出P，Q坐标，然后利用两点式写出方程判断过定点，）

 

 

 

【解析】略

 

练习册系列答案
相关题目
（2013•上海）如图，已知双曲线C1：
x2
2
-y2=1，曲线C2：|y|=|x|+1，P是平面内一点，若存在过点P的直线与C1，C2都有公共点，则称P为“C1-C2型点”
（1）在正确证明C1的左焦点是“C1-C2型点“时，要使用一条过该焦点的直线，试写出一条这样的直线的方程（不要求验证）；
（2）设直线y=kx与C2有公共点，求证|k|＞1，进而证明原点不是“C1-C2型点”；
（3）求证：圆x2+y2=
1
2
内的点都不是“C1-C2型点”

如图，已知双曲线C1：，曲线C2：|y|=|x|+1，P是平面内一点，若存在过点P的直线与C1，C2都有公共点，则称P为“C1﹣C2型点“

（1）在正确证明C1的左焦点是“C1﹣C2型点“时，要使用一条过该焦点的直线，试写出一条这样的直线的方程（不要求验证）；

（2）设直线y=kx与C2有公共点，求证|k|＞1，进而证明原点不是“C1﹣C2型点”；

（3）求证：圆x2+y2=内的点都不是“C1﹣C2型点”

 
如图，已知双曲线C1：，曲线C2：|y|=|x|+1，P是平面内一点，若存在过点P的直线与C1，C2都有公共点，则称P为“C1-C2型点“
（1）在正确证明C1的左焦点是“C1-C2型点“时，要使用一条过该焦点的直线，试写出一条这样的直线的方程（不要求验证）；
（2）设直线y=kx与C2有公共点，求证|k|＞1，进而证明原点不是“C1-C2型点”；
（3）求证：圆x2+y2=内的点都不是“C1-C2型点”
如图，已知双曲线C1：，曲线C2：|y|=|x|+1，P是平面内一点，若存在过点P的直线与C1，C2都有公共点，则称P为“C1-C2型点“
（1）在正确证明C1的左焦点是“C1-C2型点“时，要使用一条过该焦点的直线，试写出一条这样的直线的方程（不要求验证）；
（2）设直线y=kx与C2有公共点，求证|k|＞1，进而证明原点不是“C1-C2型点”；
（3）求证：圆x2+y2=内的点都不是“C1-C2型点”

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网