题目内容
2.已知向量$\overrightarrow{a}$=(sinx,$\sqrt{3}$cosx),$\overrightarrow{b}$=(cosx,-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$+$\frac{\sqrt{3}}{2}$,x∈[0,π],当方程f(x)=m有两个不同实根时.(1)求m的取值范围;
(2)求方程的两个不等实根之和.
分析 (1)将函数转化为f(x)=sin(2x-$\frac{π}{3}$),再求出f(x)的取值范围,从而求出m的范围;
(2)设出方程的两根,由两个交点关于直线2x-$\frac{π}{3}$=$\frac{π}{2}$对称,从而求出两个不等实根之和.
解答 解:(1)f(x)=sinxcosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$
=$\frac{1}{2}$sin2x-$\sqrt{3}$•$\frac{1+cos2x}{2}$+$\frac{\sqrt{3}}{2}$
=sin(2x-$\frac{π}{3}$),
∵x∈[0,π],
∴2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{5π}{3}$],
∴-$\frac{\sqrt{3}}{2}$≤f(x)≤1,
画出函数f(x)=sin(2x-$\frac{π}{3}$)的图象,
如图示: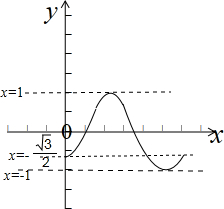
若方程f(x)=m有两个不同实根,
则-$\frac{\sqrt{3}}{2}$<m<1或-1<m<-$\frac{\sqrt{3}}{2}$;
(2)若函数f(x)的图象和直线y=m有2个交点,
设x1,x2是这两个交点的横坐标.
∵x∈[0,π],∴2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{5π}{3}$],
若这两个交点关于直线2x-$\frac{π}{3}$=$\frac{π}{2}$对称,则有x1+x2=$\frac{5π}{6}$,
若这两个交点关于直线2x-$\frac{π}{3}$=$\frac{3π}{2}$对称,则有x1+x2=$\frac{11π}{6}$,
∴方程的两个不等实根之和为$\frac{5π}{6}$或$\frac{11π}{6}$.
点评 本题主要考查了向量的运算,考查正弦函数的图象特征,体现了转化、分类讨论的数学思想,属于中档题.

 阅读快车系列答案
阅读快车系列答案