题目内容
17.已知椭圆M:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)过点(1,$\frac{\sqrt{3}}{2}$),且该椭圆的离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=x+m(m≠0)与椭圆交于A,B两点,直线l2:y=x-m与椭圆交于C,D两点.(1)求椭圆M的方程;
(2)求四边形ABCD面积的最大值.
分析 (1)将点(1,$\frac{\sqrt{3}}{2}$)带入椭圆方程,并根据离心率$e=\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}=\frac{\sqrt{3}}{2}$,这样便可得到关于a,b的方程组,解方程组即得椭圆的标准方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)先容易判断出四边形ABCD为平行四边形,所以面积为弦长|AB|与直线l1,l2之间距离的乘积,设A(x1,y1),B(x2,y2),根据弦长公式即可得到|AB|=$\frac{4\sqrt{2}}{5}•\sqrt{5-{m}^{2}}$,根据直线l1,l2的方程即可求出这两直线间的距离为$\sqrt{2}|m|$,所以得到四边形ABCD的面积为$\frac{8}{5}•|m|•\sqrt{5-{m}^{2}}$,根据基本不等式即可求该面积的最大值.
解答 解:(1)依题意可得,$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{3}{4{b}^{2}}=1}\\{\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}=\frac{\sqrt{3}}{2}}\end{array}\right.$;
解得a2=4,b2=1;
∴椭圆M的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)显然直线l1与直线l2关于原点对称,所以四边形ABCD为平行四边形;
∴|AB|=|CD|,?ABCD的面积为弦长|AB|与直线l1,l2距离的乘积;
设A(x1,y1),B(x2,y2),由$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$消去y得,5x2+8mx+4m2-4=0;
则△=16(5-m2)>0,∴0<m2<5;
根据韦达定理${x}_{1}+{x}_{2}=-\frac{8m}{5},{x}_{1}{x}_{2}=\frac{4({m}^{2}-1)}{5}$;
∴$|AB|=\sqrt{2}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}•\sqrt{\frac{80-16{m}^{2}}{25}}=\frac{4\sqrt{2}}{5}•\sqrt{5-{m}^{2}}$;
直线l1与l2的距离为$2|m|•\frac{\sqrt{2}}{2}=\sqrt{2}|m|$;
∴${S}_{四边形ABCD}=\sqrt{2}|m|•\frac{4\sqrt{2}}{5}•\sqrt{5-{m}^{2}}$=$\frac{8}{5}•|m|•\sqrt{5-{m}^{2}}≤\frac{8}{5}•\frac{{m}^{2}+5-{m}^{2}}{2}=4$;
当且仅当${m}^{2}=\frac{5}{2}$时等号成立;
∴四边形ABCD面积的最大值为4.
点评 考查椭圆的标准方程,椭圆的离心率e=$\frac{c}{a}$,以及曲线上点的坐标和曲线方程的关系,韦达定理,弦长公式,求两平行线间的距离,椭圆的对称性,以及基本不等式的运用.

 53随堂测系列答案
53随堂测系列答案 正三棱柱ABC-A1B1C1的底面面积等于$\sqrt{3}$cm2,DE分别在侧棱AA1,CC1上,且AD=AB=2CE.过点B、D、E作截面BDE.求顶点A到截面BDE的距离.
正三棱柱ABC-A1B1C1的底面面积等于$\sqrt{3}$cm2,DE分别在侧棱AA1,CC1上,且AD=AB=2CE.过点B、D、E作截面BDE.求顶点A到截面BDE的距离.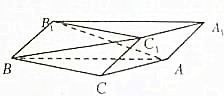 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2,
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2,