题目内容

15．求曲线f（x）=x2在x=1处的切线方程．

分析 求出导数，求得切线的斜率和切点，由点斜式方程即可得到切线方程．

解答 解：f（x）=x2的导数为f′（x）=2x，
则f（x）在x=1处的切线斜率为2，
切点为（1，1），
则有f（x）=x2在x=1处的切线方程为y-1=2（x-1），
即为2x-y-1=0．

点评 本题考查导数的运用：求切线方程，主要考查导数的几何意义：函数在某点处的导数即为曲线在该点处的切线的斜率，同时考查直线的点斜式方程，属于基础题．

练习册系列答案
相关题目
2．已知向量$\overrightarrow{a}$=（sinx，$\sqrt{3}$cosx），$\overrightarrow{b}$=（cosx，-cosx），函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$+$\frac{\sqrt{3}}{2}$，x∈[0，π]，当方程f（x）=m有两个不同实根时．
（1）求m的取值范围；
（2）求方程的两个不等实根之和．
3．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点F1（-c，0），F2（c，0），M为椭圆上的一点，且满足∠F1MF2=$\frac{π}{3}$．
（1）求椭圆离心率的取值范围；
（2）当椭圆的离心率e=$\frac{{\sqrt{2}}}{2}$，且与圆x2+y2=5相交于P（2，y0）（y0＞0）时，求此时椭圆C 的方程．
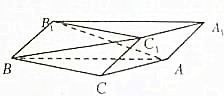10．如图，斜三棱柱ABC-A1B1C1的底面是直角三角形，∠ACB=90°，点B1在底面内的射影恰好是BC的中点，且BC=CA=2，
（1）求证：平面ACC1A1⊥平面BCC1B1；
（2）若AA1=2，求点B到平面B1CA的距离．
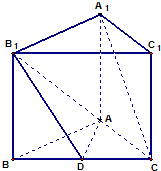20．在直三棱柱（侧棱与底面垂直的三棱柱）ABC-A1B1C1中，AB=8，AC=6，BC=10，A1A=6，D是BC边的中点．
（1）求证：AB⊥A1C；       
（2）求证：A1C∥面AB1D；
（3）求点A到面A1BC的距离．
7．已知函数f（x）=$\frac{ln（x+a）}{lnx}$．
（Ⅰ）当a=1时，求f（x）的单调区间，并比较log23，log34与log45的大小；
（Ⅱ）若实数a满足|a|≥1时，讨论f（x）极值点的个数．
4．某网站有11种资料，下载这些资料需要扣点数，其中8种资料下载一个需扣20个点，3种资料下载一个需扣10个点．某人用100个点下载资料（每种资料至多下载一个，100个点刚好用完），则不同的下载方法的种数是266．（用数字作答）
5．数列1，$\frac{1}{2}$，$\frac{1}{4}$，…$\frac{1}{{2}^{n-1}}$，…的前100项的和为2-2-99．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网