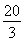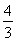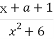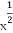题目内容
已知m=(2cos x+2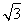 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.
(1)将y表示为x的函数f(x),并求f(x)的单调递增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f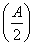 =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.
(1)单调递增区间为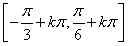 ,k∈Z(2)
,k∈Z(2)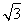
【解析】(1)由m⊥n得m·n=0,2cos2x+2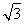 sin xcos x-y=0,
sin xcos x-y=0,
即y=2cos2x+2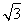 sin xcos x=cos 2x+
sin xcos x=cos 2x+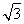 sin 2x+1=2sin
sin 2x+1=2sin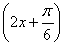 +1.
+1.
令-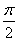 +2kπ≤2x+
+2kπ≤2x+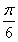 ≤
≤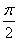 +2kπ,k∈Z,
+2kπ,k∈Z,
则-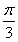 +kπ≤x≤
+kπ≤x≤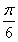 +kπ,k∈Z,
+kπ,k∈Z,
故f(x)的单调递增区间为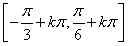 ,k∈Z.
,k∈Z.
(2)因为f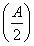 =3,所以2sin
=3,所以2sin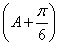 +1=3,sin
+1=3,sin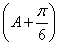 =1,
=1,
所以A+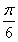 =2kπ+
=2kπ+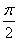 ,k∈Z.因为0<A<π,所以A=
,k∈Z.因为0<A<π,所以A=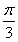 .
.
由余弦定理得:a2=b2+c2-2bccos A,即4=b2+c2-bc,
所以4=(b+c)2-3bc,
因为b+c=4,所以bc=4.所以S△ABC=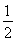 bcsin A=
bcsin A=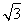 .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目