题目内容
已知焦点在x轴上,中心在坐标原点的椭圆C的离心率为 ,且过点(
,且过点(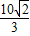 ,1).
,1).(I)求椭圆C的方程;
(II)直线l分别切椭圆C与圆M:x2+y2=R2(其中3<R<5)于A、B两点,求|AB|的最大值.
【答案】分析:(I)设出椭圆的方程,根据离心率及椭圆过点(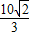 ,1)求出待定系数,即得椭圆的方程.
,1)求出待定系数,即得椭圆的方程.
(II)用斜截式设出直线的方程,代入椭圆的方程,化为关于x的一元二次方程,利用根与系数的关系,化简|AB|的解析式并利用基本不等式求出其最大值.
解答:解:(I)设椭圆的方程为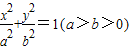 ,则
,则 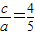 ,
,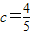 a,
a,
∴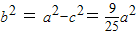 ,
,
∵椭圆过点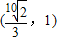 ,∴
,∴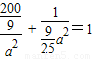 ,解得 a2=25,b2=9,
,解得 a2=25,b2=9,
故椭圆C的方程为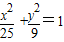 (4分)
(4分)
(II)设A(x1,y1),B(x2,y2)分别为直线l与椭圆和圆的切点,
直线AB的方程为y=kx+m,因为A既在椭圆上,又在直线AB上,
从而有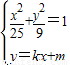 ,消去y得:(25k2+9)x2+50kmx+25(m2-9)=0,
,消去y得:(25k2+9)x2+50kmx+25(m2-9)=0,
由于直线与椭圆相切,
故△=(50kmx)2-4(25k2+9)x25(m2-9)=0,从而可得:m2=9+25k2,①,x1=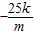 ,②
,②
由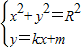 .消去y得:(k2+1)x2+2kmx+m2-R2=0,
.消去y得:(k2+1)x2+2kmx+m2-R2=0,
由于直线与圆相切,得m2=R2(1+k2),③,x2=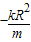 ,④
,④
由②④得:x2-x1=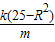 ,由①③得:k2=
,由①③得:k2=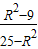 ,(9分)
,(9分)
∴|AB|2=(x2-x1)2+(y2-y1)2=(1+k2)(x2-x1)2
=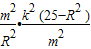 =
=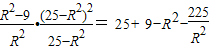
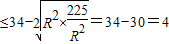
即|AB|≤2,当且仅当R=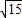 时取等号,所以|AB|的最大值为2(12分)
时取等号,所以|AB|的最大值为2(12分)
点评:本题考查用待定系数法求椭圆的标准方程,一元二次方程根与系数的关系,基本不等式的应用.
 ,1)求出待定系数,即得椭圆的方程.
,1)求出待定系数,即得椭圆的方程.(II)用斜截式设出直线的方程,代入椭圆的方程,化为关于x的一元二次方程,利用根与系数的关系,化简|AB|的解析式并利用基本不等式求出其最大值.
解答:解:(I)设椭圆的方程为
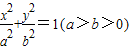 ,则
,则 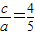 ,
,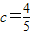 a,
a,∴
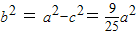 ,
,∵椭圆过点
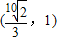 ,∴
,∴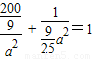 ,解得 a2=25,b2=9,
,解得 a2=25,b2=9,故椭圆C的方程为
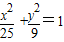 (4分)
(4分)(II)设A(x1,y1),B(x2,y2)分别为直线l与椭圆和圆的切点,
直线AB的方程为y=kx+m,因为A既在椭圆上,又在直线AB上,
从而有
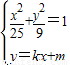 ,消去y得:(25k2+9)x2+50kmx+25(m2-9)=0,
,消去y得:(25k2+9)x2+50kmx+25(m2-9)=0,由于直线与椭圆相切,
故△=(50kmx)2-4(25k2+9)x25(m2-9)=0,从而可得:m2=9+25k2,①,x1=
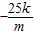 ,②
,②由
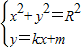 .消去y得:(k2+1)x2+2kmx+m2-R2=0,
.消去y得:(k2+1)x2+2kmx+m2-R2=0,由于直线与圆相切,得m2=R2(1+k2),③,x2=
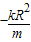 ,④
,④由②④得:x2-x1=
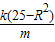 ,由①③得:k2=
,由①③得:k2=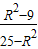 ,(9分)
,(9分)∴|AB|2=(x2-x1)2+(y2-y1)2=(1+k2)(x2-x1)2
=
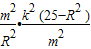 =
=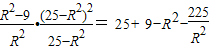
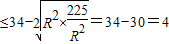
即|AB|≤2,当且仅当R=
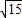 时取等号,所以|AB|的最大值为2(12分)
时取等号,所以|AB|的最大值为2(12分)点评:本题考查用待定系数法求椭圆的标准方程,一元二次方程根与系数的关系,基本不等式的应用.

练习册系列答案
相关题目
 已知椭圆的中心在坐标原点,焦点在x轴上,并且焦距为2,短轴与长轴的比是
已知椭圆的中心在坐标原点,焦点在x轴上,并且焦距为2,短轴与长轴的比是