题目内容
(2008•深圳二模)已知椭圆C的中心在原点,焦点在x轴上,点F1、F2分别是椭圆的左、右焦点,在椭圆C的右准线上的点P(2,
),满足线段PF1的中垂线过点F2.直线l:y=kx+m为动直线,且直线l与椭圆C交于不同的两点A、B.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足
+
=λ
(O为坐标原点),求实数λ的取值范围;
(Ⅲ)在(Ⅱ)的条件下,当λ取何值时,△ABO的面积最大,并求出这个最大值.
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足
| OA |
| OB |
| OQ |
(Ⅲ)在(Ⅱ)的条件下,当λ取何值时,△ABO的面积最大,并求出这个最大值.
分析:(Ⅰ)利用待定系数法求椭圆的方程,设椭圆C的方程为
+
=1(a>b>0),根据在椭圆C的右准线上的点P(2,
),满足线段PF1的中垂线过点F2.可得几何量之间的关系,进而可得椭圆方程;
(Ⅱ)减法直线方程与椭圆方程联立
,消去y得(1+2k2)x2+4kmx+2m2-2=0.设点A、B的坐标分别为A(x1,y1)、B(x2,y2),由此可得
,根据
+
=λ
,可得
利用点Q在椭圆上,可得方程4m2(1+2k2)=λ2(1+2k2)2.进而可确定实数λ的取值范围
(Ⅲ)由于|AB|=
|x1-x2|,点O到直线AB的距离d=
,故可表示△AOB的面积,可整理成关于λ的函数S=
,进而可求△ABO的面积最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅱ)减法直线方程与椭圆方程联立
|
|
| OA |
| OB |
| OQ |
|
利用点Q在椭圆上,可得方程4m2(1+2k2)=λ2(1+2k2)2.进而可确定实数λ的取值范围
(Ⅲ)由于|AB|=
| 1+k2 |
| |m| | ||
|
| ||
| 4 |
| λ2(4-λ2) |
解答:解:(Ⅰ)设椭圆C的方程为
+
=1(a>b>0),半焦距为c,
依题意有
解得
∴b=1.
∴所求椭圆方程为
+y2=1. …3分
(Ⅱ)由
,得(1+2k2)x2+4kmx+2m2-2=0.
设点A、B的坐标分别为A(x1,y1)、B(x2,y2),
则
…5分y1+y2=k(x1+x2)+2m=
.
(1)当m=0时,点A、B关于原点对称,则λ=0.
(2)当m≠0时,点A、B不关于原点对称,则λ≠0,
由
+
=λ
,得
即
∵点Q在椭圆上,
∴有[
]2+2[
]2=2,
化简,得4m2(1+2k2)=λ2(1+2k2)2.
∵1+2k2≠0,
∴有4m2=λ2(1+2k2).…①…7分
又∵△=16k2m2-4(1+2k2)(2m2-2)=8(1+2k2-m2),
∴由△>0,得1+2k2>m2.…②…8分
将①、②两式,得φ(x)=2elnx(e.∵m≠0,∴λ2<4,则-2<λ<2且λ≠0.
综合(1)、(2)两种情况,得实数λ的取值范围是-2<λ<2. …9分
注:此题可根据图形得出当m=0时λ=0,当A、B两点重合时λ=±2.
如果学生由此得出λ的取值范围是-2<λ<2可酌情给分.
(Ⅲ)∵|AB|=
|x1-x2|,点O到直线AB的距离d=
,
∴△AOB的面积S=
|m||x1-x2|=
|m|
=
. …12分
由①有1+2k2=
,代入上式并化简,得S=
.∵
≤2,
∴S≤
. …13分
当且仅当λ2=4-λ2,即λ=±
时,等号成立.
∴当λ=±
时,△ABO的面积最大,最大值为
. …14分.
| x2 |
| a2 |
| y2 |
| b2 |
依题意有
|
解得
|
∴b=1.
∴所求椭圆方程为
| x2 |
| 2 |
(Ⅱ)由
|
设点A、B的坐标分别为A(x1,y1)、B(x2,y2),
则
|
| 2m |
| 1+2k2 |
(1)当m=0时,点A、B关于原点对称,则λ=0.
(2)当m≠0时,点A、B不关于原点对称,则λ≠0,
由
| OA |
| OB |
| OQ |
|
|
∵点Q在椭圆上,
∴有[
| -4km |
| λ(1+2k2) |
| 2m |
| λ(1+2k2) |
化简,得4m2(1+2k2)=λ2(1+2k2)2.
∵1+2k2≠0,
∴有4m2=λ2(1+2k2).…①…7分
又∵△=16k2m2-4(1+2k2)(2m2-2)=8(1+2k2-m2),
∴由△>0,得1+2k2>m2.…②…8分
将①、②两式,得φ(x)=2elnx(e.∵m≠0,∴λ2<4,则-2<λ<2且λ≠0.
综合(1)、(2)两种情况,得实数λ的取值范围是-2<λ<2. …9分
注:此题可根据图形得出当m=0时λ=0,当A、B两点重合时λ=±2.
如果学生由此得出λ的取值范围是-2<λ<2可酌情给分.
(Ⅲ)∵|AB|=
| 1+k2 |
| |m| | ||
|
∴△AOB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
| ||||
| 1+2k2 |
由①有1+2k2=
| 4m2 |
| λ2 |
| ||
| 4 |
| λ2(4-λ2) |
| λ2(4-λ2) |
∴S≤
| ||
| 2 |
当且仅当λ2=4-λ2,即λ=±
| 2 |
∴当λ=±
| 2 |
| ||
| 2 |
点评:本题的考点是直线与圆锥曲线的综合问题,主要考查待定系数法求圆锥曲线的方程,要注意椭圆的三个参数的关系为:a2=b2+c2;求解直线与椭圆的位置关系问题,通常是联立方程组,利用韦达定理求解.

练习册系列答案
相关题目
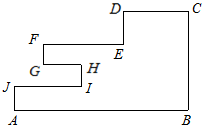 (2008•深圳二模)一个质点从A出发依次沿图中线段到达B、C、D、E、F、G、H、I、J各点,最后又回到A(如图所示),其中:AB⊥BC,AB∥CD∥EF∥HG∥IJ,BC∥DE∥FG∥HI∥JA.欲知此质点所走路程,至少需要测量n条线段的长度,则n=( )
(2008•深圳二模)一个质点从A出发依次沿图中线段到达B、C、D、E、F、G、H、I、J各点,最后又回到A(如图所示),其中:AB⊥BC,AB∥CD∥EF∥HG∥IJ,BC∥DE∥FG∥HI∥JA.欲知此质点所走路程,至少需要测量n条线段的长度,则n=( )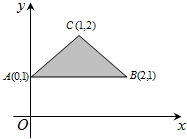 (2008•深圳二模)当点M(x,y)在如图所示的三角形ABC内(含边界)运动时,目标函数z=kx+y取得最大值的一个最优解为(1,2),则实数k的取值范围是( )
(2008•深圳二模)当点M(x,y)在如图所示的三角形ABC内(含边界)运动时,目标函数z=kx+y取得最大值的一个最优解为(1,2),则实数k的取值范围是( )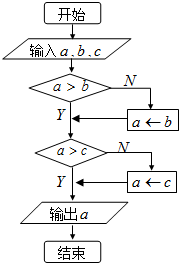 (2008•深圳二模)如图所示的算法中,令a=tanθ,b=sinθ,c=cosθ,若在集合
(2008•深圳二模)如图所示的算法中,令a=tanθ,b=sinθ,c=cosθ,若在集合