题目内容
（2012•山东）若不等式|kx-4|≤2的解集为{x|1≤x≤3}，则实数k=
2
2
．分析：|kx-4|≤2?（kx-4）2≤4，由题意可知1和3是方程k2x2-8kx+12=0的两根，有韦达定理即可求得k的值．
解答：解：∵|kx-4|≤2，
∴（kx-4）2≤4，即k2x2-8kx+12≤0，
∵不等式|kx-4|≤2的解集为{x|1≤x≤3}，
∴1和3是方程k2x2-8kx+12=0的两根，
∴1+3=
，
∴k=2．
故答案为2．
∴（kx-4）2≤4，即k2x2-8kx+12≤0，
∵不等式|kx-4|≤2的解集为{x|1≤x≤3}，
∴1和3是方程k2x2-8kx+12=0的两根，
∴1+3=
| 8k |
| k2 |
∴k=2．
故答案为2．
点评：本题考查绝对值不等式，将|kx-4|≤2转化为（kx-4）2≤4是关键，考查等价转化的思想与利用韦达定理解决问题的能力，属于基础题．，
练习册系列答案
相关题目
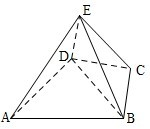（2012•山东）如图，几何体E-ABCD是四棱锥，△ABD为正三角形，CB=CD，EC⊥BD．