题目内容
(2012•山东)若θ∈[
,
],sin2θ=
,则sinθ=( )
| π |
| 4 |
| π |
| 2 |
3
| ||
| 8 |
分析:结合角的范围,通过平方关系求出二倍角的余弦函数值,通过二倍角公式求解即可.
解答:解:因为sin2θ=
,θ∈[
,
],
所以cos2θ=-
=-
,
所以1-2sin2θ=-
,
所以sin2θ=
,θ∈[
,
],
所以sinθ=
.
故选D.
3
| ||
| 8 |
| π |
| 4 |
| π |
| 2 |
所以cos2θ=-
| 1-sin22θ |
| 1 |
| 8 |
所以1-2sin2θ=-
| 1 |
| 8 |
所以sin2θ=
| 9 |
| 16 |
| π |
| 4 |
| π |
| 2 |
所以sinθ=
| 3 |
| 4 |
故选D.
点评:本题考查二倍角的正弦,同角三角函数间的基本关系,注意角的范围,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
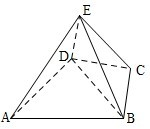 (2012•山东)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(2012•山东)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.