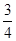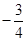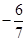题目内容
《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样的一道题目:把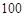 个面包分给
个面包分给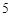 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的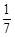 是较小的两份之和,则最小的
是较小的两份之和,则最小的 份为
份为
A.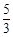 | B. | C.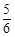 | D.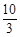 |
A
解析试题分析:设五个人所分得的面包为a-2d,a-d,a,a+d,a+2d,(d>0);则由五个人的面包和为100,得a的值;由较大的三份之和的 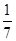 ,较小的两份之和,得d的值;从而得最小的1分a-2d的值
,较小的两份之和,得d的值;从而得最小的1分a-2d的值
五个人所分得的面包为a-2d,a-d,a,a+d,a+2d,(其中d>0)
则,(a-2d)+(a-d)+a+(a+d)+(a+2d)=5a=100,∴a=20;
由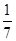 (a+a+d+a+2d)=a-2d+a-d,得3a+3d=7(2a-3d);∴24d=11a,∴d=55/6;
(a+a+d+a+2d)=a-2d+a-d,得3a+3d=7(2a-3d);∴24d=11a,∴d=55/6;
所以,最小的1分为a-2d=20-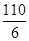 =
=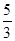 ,选A
,选A
考点:等差数列
点评:本题考查了等差数列模型的实际应用,解题时应巧设数列的中间项,从而容易得出结果

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
等差数列{an}和{bn}的前n项和分别为Sn和Tn,且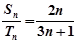 ,则
,则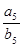 ( )
( )
A.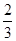 | B.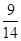 | C.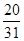 | D.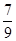 |
已知等差数列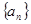 的公差为
的公差为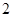 ,若
,若 成等比数列, 则
成等比数列, 则 ( )
( )
A.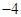 | B.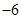 | C.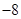 | D.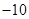 |
数列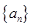 的首项为
的首项为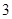 ,
,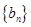 为等差数列且
为等差数列且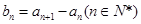 .若则
.若则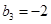 ,
,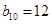 ,则
,则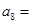 ( )
( )
| A.0 | B.3 | C.8 | D.11 |
已知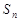 是等差数列
是等差数列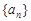 的前
的前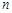 项和,若
项和,若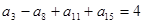 ,则
,则 的值是
的值是
| A.5 | B.8 | C.16 | D.20 |
在等差数列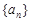 中,已知
中,已知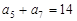 ,则该数列前11项和
,则该数列前11项和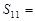
| A.196 | B.132 | C.88 | D.77 |
数列 是等差数列,
是等差数列,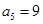 ,
, ,则
,则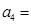
A.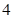 | B.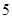 | C.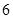 | D.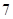 |
设等差数列 的公差不等于0,且其前n项和为
的公差不等于0,且其前n项和为 。若
。若 且
且 成等比数列,则
成等比数列,则
| A.40 | B.54 | C.80 | D.96 |
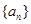 中,
中,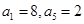 ,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差是( )
,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差是( )