题目内容
如图，在△ABC中，G是△ABC的重心，证明：| AG |
| 1 |
| 3 |
| AB |
| AC |
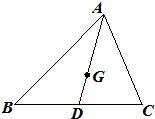
分析：本题可以作出辅助线取AC中点E，连接DE，利用中位线性质，三角形相似，得出AG=
AD，再利用向量共线定理
=
来解答．
| 2 |
| 3 |
| AG |
| 2 |
| 3 |
| AD |
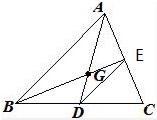
解答：证明：如图取AC中点E，连接DE，则DE∥AB，且DE=
AB，
易得△GDE∽△GAB，所以DG=
AG，从而AG=
AD
由向量加法的平行四边形法则得：
=
(
+
)，
与
共线，
所以
=
，即：
=
•
(
+
)=
(
+
)
| 1 |
| 2 |
易得△GDE∽△GAB，所以DG=
| 1 |
| 2 |
| 2 |
| 3 |
由向量加法的平行四边形法则得：
| AD |
| 1 |
| 2 |
| AB |
| AC |
| AG |
| AD |
所以
| AG |
| 2 |
| 3 |
| AD |
| AG |
| 2 |
| 3 |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 3 |
| AB |
| AC |
点评：本题考查向量加法及三角形，平行四边形法则，共线向量定理和平面向量基本定理的应用，利用向量基底表示平面内向量的方法．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在△ABC中，设
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
如图，在△ABC中，已知