题目内容
线段∣AB∣=4,∣PA∣+∣PB∣=6,M是AB的中点,当P点在同一平面内运动时,PM的长度的最小值是( )
| A.2 | B.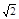 | C.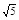 | D.5 |
C
解析考点:椭圆的简单性质.
分析:利用椭圆的定义和性质,数形结合,结合M是AB的中点,可得M(0,0),从而可求|PM|的最小值.
解:∵线段|AB|=4,|PA|+|PB|=6,
∴动点P在以A、B为焦点、长轴等于6的椭圆上,a=3,c=2,
∴b=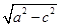 =
=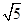
∵M是AB的中点,
∴M(0,0)
∴|PM|的最小值是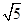
故选C.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
以椭圆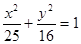 的焦点为顶点,离心率为
的焦点为顶点,离心率为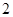 的双曲线方程( )
的双曲线方程( )
A.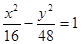 | B.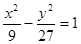 |
C.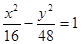 或 或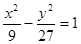 | D.以上都不对 |
已知双曲线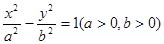 的左右焦点分别 为F1、F2,P是准线上一点,且
的左右焦点分别 为F1、F2,P是准线上一点,且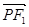 ·
·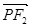 =0,
=0,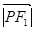 ·
·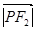 =4ab,则双曲线的离心率是
=4ab,则双曲线的离心率是
A.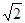 | B.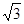 | C.2 | D.3 |
.已知点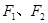 为椭圆
为椭圆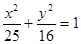 的左右焦点,过
的左右焦点,过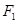 的直线
的直线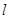 交该椭圆于
交该椭圆于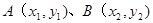 两点,
两点,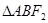 的内切圆的周长为
的内切圆的周长为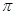 ,则
,则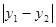 的值是( )
的值是( )
A.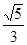 | B.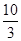 | C.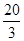 | D.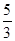 |
以 为准线的抛物线的标准方程为 ( )
为准线的抛物线的标准方程为 ( )
A.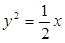 | B.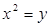 | C.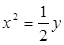 | D.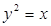 |
如果椭圆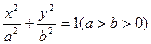 的离心率为
的离心率为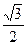 ,那么双曲线
,那么双曲线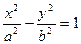 的离心率是 ( )
的离心率是 ( )
A.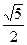 | B. | C.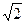 | D.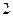 |
 的焦点为
的焦点为 ,
, 在抛物线上,且
在抛物线上,且 ,弦
,弦 的中点
的中点
 在其准线上的射影为
在其准线上的射影为 ,则
,则 的最大值为( )
的最大值为( )



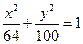 的准线方程是
的准线方程是
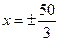

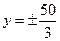

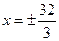

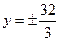
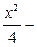 y2=1两个焦点,点P在双曲线上,满足∠F1PF2=90°,则△F1PF2的面积是( )
y2=1两个焦点,点P在双曲线上,满足∠F1PF2=90°,则△F1PF2的面积是( )