��Ŀ����
13��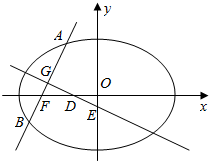 ��ͼ����Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$����ΪF������F��ֱ�߽���Բ��A��B���㣬|AF|�����ֵΪM��|BF|����СֵΪm������$M•m=\frac{3}{4}{a^2}$��
��ͼ����Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$����ΪF������F��ֱ�߽���Բ��A��B���㣬|AF|�����ֵΪM��|BF|����СֵΪm������$M•m=\frac{3}{4}{a^2}$���������߶�AB��ֱ��x��ʱ��|AB|=$\frac{3}{2}$������Բ�ķ��̣�
���� ���߶�AB���е�ΪG��AB�Ĵ�ֱƽ������x���y��ֱ���D��E���㣬O������ԭ�㣬�ǡ�GFD�����ΪS1����OED�����ΪS2����$\frac{{2{S_1}{S_2}}}{{{S_1}^2+{S_2}^2}}$��ȡֵ��Χ��
���� ���� ��F��-c��0����c��0�����������Բ���ʵ�M=a+c��m=a-c������������ⷽ�̿ɵ�a��c��b�������õ���Բ���̣�
���������Բ����Ϊ$\frac{{x}^{2}}{4{c}^{2}}$+$\frac{{y}^{2}}{3{c}^{2}}$=1����ֱ��AB�ķ���Ϊy=k��x+c��������A��x1��y1����B��x2��y2����������Բ���̣���Τ�ﶨ�����е����깫ʽ�ɵ�G�����꣬�������������Ƶ����ʣ��ɵ������Ϊ��Ӧ�ߵ�ƽ���ȣ���ϲ���ʽ�����ʼ��ɵõ�����Χ��
��� �⣺���� ��F��-c��0����c��0�����������Բ���ʵ�
M=a+c��m=a-c��M•m=$\frac{3}{4}$a2��
������a2-c2=$\frac{3}{4}$a2����a2=4c2����a=2c��
��$\frac{{2{b^2}}}{a}=\frac{3}{2}$��a2=b2+c2��
��$a=1��{b^2}=\frac{3}{4}$��
�����Բ�ķ���Ϊ��${x^2}+\frac{{4{y^2}}}{3}=1$��
�����ɣ���֪a=2c��b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$c����Բ�ķ���Ϊ$\frac{{x}^{2}}{4{c}^{2}}$+$\frac{{y}^{2}}{3{c}^{2}}$=1��
��������ֱ��AB��б��һ�������Ҳ�Ϊ�㣬��ֱ��AB�ķ���Ϊy=k��x+c����
����A��x1��y1����B��x2��y2����
����$\left\{\begin{array}{l}y=k��x+c��\\ \frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1\end{array}\right.$��ȥy�������ã���4k2+3��x2+8ck2x+4k2c2-12c2=0��
�Ӷ���${x_1}+{x_2}=-\frac{{8c{k^2}}}{{4{k^2}+3}}��{y_1}+{y_2}=k��{x_1}+{x_2}+2c��=\frac{6ck}{{4{k^2}+3}}$��
����$G��-\frac{{4c{k^2}}}{{4{k^2}+3}}��\frac{3ck}{{4{k^2}+3}}��$��
��ΪDG��AB������$\frac{{\frac{3ck}{{4{k^2}+3}}}}{{-\frac{{4c{k^2}}}{{4{k^2}+3}}-{x_D}}}•k=-1$����${x_D}=-\frac{{c{k^2}}}{{4{k^2}+3}}$��
��Rt��FGD��Rt��EOD���ƣ�
����$\frac{S_1}{S_2}=\frac{{G{D^2}}}{{O{D^2}}}=\frac{{{{��-\frac{{4c{k^2}}}{{4{k^2}+3}}+\frac{{c{k^2}}}{{4{k^2}+3}}��}^2}+{{��\frac{3ck}{{4{k^2}+3}}��}^2}}}{{{{��-\frac{{c{k^2}}}{{4{k^2}+3}}��}^2}}}=9+\frac{9}{k^2}��9$��
��$\frac{S_1}{S_2}=t$����t��9��
�Ӷ�$\frac{{2{S_1}{S_2}}}{{{S_1}^2+{S_2}^2}}=\frac{2}{{t+\frac{1}{t}}}��\frac{2}{{9+\frac{1}{9}}}=\frac{9}{41}$��
��$\frac{{2{S_1}{S_2}}}{{{S_1}^2+{S_2}^2}}$��ȡֵ��Χ��$��0��\frac{9}{41}��$��
���� ���⿼����Բ�ķ��̵���ע��������Բ�����ʣ�����ֱ�ߺ���Բ��������������Τ�ﶨ����ֱ�ߴ�ֱ��������б��֮��Ϊ-1���������������Ƶ����ʣ������ε����֮��Ϊ���Ʊȵ�ƽ�������黯�����������������������е��⣮

 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�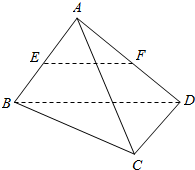 �ڿռ��ı���ABCD�У�E��F�ֱ���AB��AD���е�
�ڿռ��ı���ABCD�У�E��F�ֱ���AB��AD���е�