题目内容
已知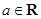 ,函数
,函数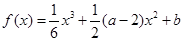 ,
,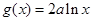 .
.
(1)若曲线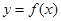 与曲线
与曲线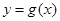 在它们的交点
在它们的交点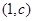 处的切线互相垂直,求
处的切线互相垂直,求 ,
,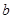 的值;
的值;
(2)设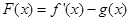 ,若对任意的
,若对任意的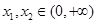 ,且
,且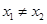 ,都有
,都有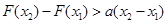 ,求
,求 的取值范围.
的取值范围.
(1)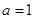 ,或
,或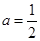 ;(2)
;(2)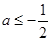 .
.
解析试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求曲线的切线等基础知识,考查学生的分析问题解决问题的能力、计算能力、转化能力.第一问,由于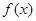 与
与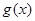 在
在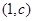 处的切线互相垂直,所以两条切线相互垂直,即斜率相乘得-1,对
处的切线互相垂直,所以两条切线相互垂直,即斜率相乘得-1,对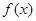 和
和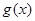 求导,将1代入得到两切线的斜率,列出方程得出a的值;第二问,先将“对任意的
求导,将1代入得到两切线的斜率,列出方程得出a的值;第二问,先将“对任意的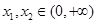 ,且
,且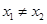 ,都有
,都有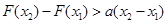 ”转化为“对任意的
”转化为“对任意的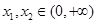 ,且
,且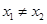 ,都有
,都有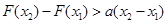 ”,令
”,令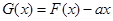 ,则原命题等价于
,则原命题等价于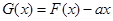 在
在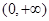 是增函数,对
是增函数,对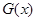 求导,判断导数的正负,决定函数的单调性.
求导,判断导数的正负,决定函数的单调性.
(1)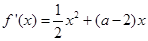 ,
,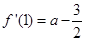 .
.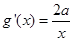 ,
,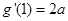 .
.
依题意有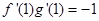 ,
,
可得 ,解得
,解得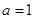 ,或
,或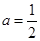 . 6分
. 6分
(2)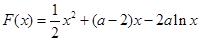 .
.
不妨设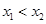 ,
,
则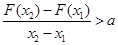 等价于
等价于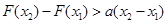 ,
,
即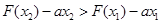 .
.
设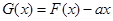 ,
,
则对任意的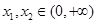 ,且
,且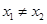 ,都有
,都有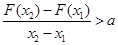 ,
,
等价于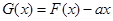 在
在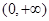 是增函数.
是增函数.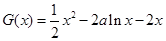 ,
,
可得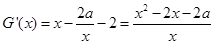 ,
,
依题意有,对任意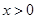 ,有
,有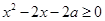 .
.
由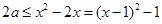 ,可得
,可得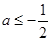 . 13分
. 13分
考点:导数的运算、利用导数判断函数的单调性、利用导数求曲线的切线.

练习册系列答案
相关题目
 ,求函数f(x)和f′(x)的公共递减区间的长度;
,求函数f(x)和f′(x)的公共递减区间的长度; ,曲线
,曲线 在点
在点 处的切线与直线
处的切线与直线 垂直.
垂直. 的值;
的值; ,
, 恒成立,求
恒成立,求 的范围;
的范围;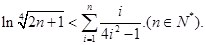
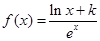 (其中
(其中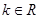 ),
),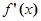 为f(x)的导函数.
为f(x)的导函数.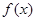 在点(1,
在点(1,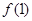 )处的切线不过点(2,0);
)处的切线不过点(2,0);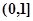 中存在
中存在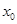 ,使得
,使得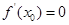 ,求
,求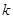 的取值范围;
的取值范围;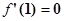 ,试证明:对任意
,试证明:对任意 ,
,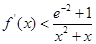 恒成立.
恒成立. ,
, .
. 的单调区间;
的单调区间;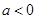 时,若对于任意的
时,若对于任意的 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围.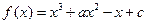 ,且
,且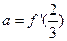 .
. 的值;
的值;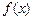 的单调区间;
的单调区间;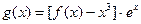 ,若函数
,若函数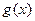 在
在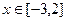 上单调递增,求实数
上单调递增,求实数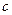 的取值范围.
的取值范围.