题目内容
【题目】已知椭圆![]() ,点
,点![]() ,
,
![]() 中恰有三点在椭圆
中恰有三点在椭圆![]() 上.
上.
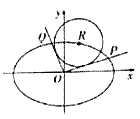
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上的动点,由原点
上的动点,由原点![]() 向圆
向圆![]() 引两条切线,分别交椭圆于点
引两条切线,分别交椭圆于点![]() ,若直线
,若直线![]() 的斜率存在,并记为
的斜率存在,并记为![]() ,试问
,试问![]() 的面积是否为定值?若是,求出该值;若不是,请说明理由.
的面积是否为定值?若是,求出该值;若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据对称性可知椭圆C经过P3,P4两点,则图象不经过点P1,故P2在椭圆上,代入点坐标可求出椭圆方程;
(2)由直线OP:y=k1x,OQ:y=k2x与圆M相切,运用圆心到直线的距离为半径,即可得到k1,k2为方程(x02﹣2)k2﹣2x0y0k+y02﹣2=0的两个不等的实根,运用韦达定理和点M在椭圆上,满足椭圆方程,化简即可得到k1k2=﹣![]() ,设P(x1,y1),Q(x2,y2),表示出△OPQ的面积S=
,设P(x1,y1),Q(x2,y2),表示出△OPQ的面积S=![]() |x1x2||k1﹣k2|,代值计算即可求出.
|x1x2||k1﹣k2|,代值计算即可求出.
解:(1)由于P3,P4两点关于原点对称,故由题设可知C经过P3,P4两点,
∵![]() ,
,
则图象不经过点P1,故P2在椭圆上,
∴b=![]() ,
,![]() ,解得a2=6,b2=3,
,解得a2=6,b2=3,
故椭圆C的方程为![]() .
.
(2)∵直线OP:y=k1x,OQ:y=k2x,与圆M相切,
由直线和圆相切的条件:d=r,可得![]() ,
,
即有(x02﹣2)k12﹣2x0y0k1+y02﹣2=0,
同理:直线OQ:y=k2x与圆M相切,
可得(x02﹣2)k22﹣2x0y0k2+y02﹣2=0,
即k1,k2为方程(x02﹣2)k2﹣2x0y0k+y02﹣2=0的两个不等的实根,
可得k1k2=![]() ,
,
∵点R(x0,y0)在椭圆C上,
∴![]() ,
,
∴k1k2=![]() =
=![]() ,
,
设P(x1,y1),Q(x2,y2),
∴|OP|=![]() |x1|
|x1|
点Q到直线OP的距离d=![]() ,
,
∵|x1|=![]() ,|x2|=
,|x2|=![]() ,
,
∴△OPQ的面积S=![]() |x1x2||k1﹣k2|=
|x1x2||k1﹣k2|=![]()
![]()
![]()
![]() ,
,
=![]() .
.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:
年龄x | 28 | 32 | 38 | 42 | 48 | 52 | 58 | 62 |
收缩压 | 114 | 118 | 122 | 127 | 129 | 135 | 140 | 147 |
其中: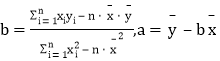 ,
,![]() ,
,![]()

![]() 请画出上表数据的散点图;
请画出上表数据的散点图;
![]() 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;![]() 的值精确到
的值精确到![]()
![]() 若规定,一个人的收缩压为标准值的
若规定,一个人的收缩压为标准值的![]() 倍,则为血压正常人群;收缩压为标准值的
倍,则为血压正常人群;收缩压为标准值的![]() 倍,则为轻度高血压人群;收缩压为标准值的
倍,则为轻度高血压人群;收缩压为标准值的![]() 倍,则为中度高血压人群;收缩压为标准值的
倍,则为中度高血压人群;收缩压为标准值的![]() 倍及以上,则为高度高血压人群
倍及以上,则为高度高血压人群![]() 一位收缩压为180mmHg的70岁的老人,属于哪类人群?
一位收缩压为180mmHg的70岁的老人,属于哪类人群?