题目内容
【题目】选修4-5:不等式选讲
已知f(x)=|x+a|(a∈R).
(1)若f(x)≥|2x﹣1|的解集为[0,2],求a的值;
(2)若对任意x∈R,不等式f(x)+|x﹣a|≥3a﹣2恒成立,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用两边平方解含有绝对值的不等式,再根据根与系数的关系求出a的值;
(2)利用绝对值不等式求出f(x)+|x﹣a|的最小值,把不等式f(x)+|x﹣a|≥3a﹣2化为只含有a的不等式,求出不等式解集即可.
(1)不等式f(x)≥|2x﹣1|,即|x+a|≥|2x﹣1|,
两边平方整理得3x2﹣(2a+4)x+1﹣a2≤0,
由题意知0和2是方程3x2﹣(2a+4)x+1﹣a2=0的两个实数根,
即 ,解得a=1;
,解得a=1;
(2)因为f(x)+|x﹣a|=|x+a|+|x﹣a|≥|(x+a)﹣(x﹣a)|=2|a|,
所以要使不等式f(x)+|x﹣a|≥3a﹣2恒成立,只需2|a|≥3a﹣2,
当a≥0时,2a≥3a﹣2,解得a≤2,即0≤a≤2;
当a<0时,﹣2a≥3a﹣2,解得a≤![]() ,即a<0;
,即a<0;
综上所述,a的取值范围是(﹣∞,2].

 名校课堂系列答案
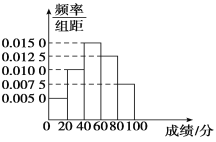
名校课堂系列答案【题目】某中学准备组建“文科”兴趣特长社团,由课外活动小组对高一学生文科、理科进行了问卷调查,问卷共100道题,每题1分,总分100分,该课外活动小组随机抽取了200名学生的问卷成绩(单位:分)进行统计,将数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
|
|
(1)根据已知条件完成下面![]() 列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
(2)将频率视为概率,现在从该校高一学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“文科方向”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
参考公式: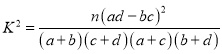 ,其中
,其中![]() .
.
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样,回答问题统计结果如图表所示.

组别 | 分组 | 回答正确的人数 | 回答正确的人数占本组的概率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) |
| 0.9 |
第3组 | [35,45) | 27 |
|
第4组 | [45,55) |
| 0.36 |
第5组 | [55,65) | 3 |
|
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.