题目内容
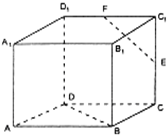如图，正方体ABCD-A1B1C1D1中，E、F分别是CC1、C1D1的中点，则异面直线EF和BD所成的角的大小为 （ ）分析：连接D1C，D1B1，B1C，得到∠B1D1C是异面直线EF和BD所成的角（或所成角的补角），由此能求出异面直线EF和BD所成的角的大小．
解答：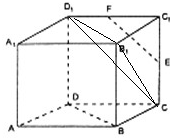
解：连接D1C，D1B1，B1C，
∵E、F分别是CC1、C1D1的中点，
∴EF∥D1C，
∵BD∥D1B1，
∴∠B1D1C是异面直线EF和BD所成的角（或所成角的补角），
∵正方体ABCD-A1B1C1D1中，D1B1=B1C=D1C，
∴∠B1D1C=60°．
故选B．
解：连接D1C，D1B1，B1C，∵E、F分别是CC1、C1D1的中点，
∴EF∥D1C，
∵BD∥D1B1，
∴∠B1D1C是异面直线EF和BD所成的角（或所成角的补角），
∵正方体ABCD-A1B1C1D1中，D1B1=B1C=D1C，
∴∠B1D1C=60°．
故选B．
点评：本题考查异面直线所成角的大小的求法，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，正方体ABCD-A1B1C1D1中，E，F分别为BB1和A1D1的中点．证明：向量
如图，正方体ABCD-A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．
如图，正方体ABCD-A1B1C1D1中，若E、F、G分别为棱BC、C1C、B1C1的中点，O1、O2分别为四边形ADD1A1、A1B1C1D1的中心，则下列各组中的四个点不在同一个平面上的是（ ）
如图，正方体ABCD-A1B1C1D1中，E、F、G、H分别是所在棱的三等分点，且