题目内容
在抛物线y=x2+ax-5（a≠0）上取横坐标为x1=-4，x2=2的两点，经过两点引一条割线，有平行于该割线的一条直线同时与抛物线和圆5x2+5y2=36相切，则抛物线顶点的坐标为（ ）
| A．（-2，-9） | B．（0，-5） | C．（2，-9） | D．（1，6） |
两点坐标为（-4，11-4a）；（2，2a-1）
两点连线的斜率k=
=a-2
对于y=x2+ax-5
y′=2x+a
∴2x+a=a-2解得x=-1
在抛物线上的切点为（-1，-a-4）
切线方程为（a-2）x-y-6=0
直线与圆相切，圆心（0，0）到直线的距离=圆半径
=
解得a=4或0（0舍去）
抛物线方程为y=x2+4x-5顶点坐标为（-2，-9）
故选A．
两点连线的斜率k=
| 11-4a-2a+1 |
| -4-2 |
对于y=x2+ax-5
y′=2x+a
∴2x+a=a-2解得x=-1
在抛物线上的切点为（-1，-a-4）
切线方程为（a-2）x-y-6=0
直线与圆相切，圆心（0，0）到直线的距离=圆半径
| 6 | ||
|
|
解得a=4或0（0舍去）
抛物线方程为y=x2+4x-5顶点坐标为（-2，-9）
故选A．
练习册系列答案
相关题目
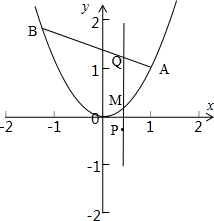设λ＞0，点A的坐标为（1，1），点B在抛物线y=x2上运动，点Q满足