题目内容
三角形ABC的两顶点A(-2,0),B(0,-2),第三顶点C在抛物线y=x2+1 上,求三角形ABC的重心G的轨迹.分析:设G(x,y),欲求△ABC的重心G的轨迹方程,即求出其坐标x,y的关系式即可,利用重心坐标公式表示出点C的坐标,最后根据第三顶点C在抛物线上运动,得出关于x,y的方程即可.
解答:解:设记G(x,y),C(x0,y0),
由重心坐标公式得
x=
,y=
所以x0=3x+2,y0=3y+2
因为C(x0,y0),
在y=x2+1 上
所3y+2=(3x+2)2+1 整理得y=3(x+
)2-
所以G点的轨迹为开口向上的抛物线.
由重心坐标公式得
x=
| -2+x 0 |
| 3 |
| -2+y 0 |
| 3 |
所以x0=3x+2,y0=3y+2
因为C(x0,y0),
在y=x2+1 上
所3y+2=(3x+2)2+1 整理得y=3(x+
| 2 |
| 3 |
| 1 |
| 3 |
所以G点的轨迹为开口向上的抛物线.
点评:充分利用第三顶点C在抛物线挖掘出动点所满足的条件是本题的关键,本题直接将动点满足的几何等量关系“翻译”成动点x,y,得方程,即为所求动点的轨迹方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
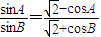 .
.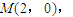 N(1,0),过N的直线与曲线E的交点是D、E.求kDM+kEM的值.
N(1,0),过N的直线与曲线E的交点是D、E.求kDM+kEM的值.