题目内容
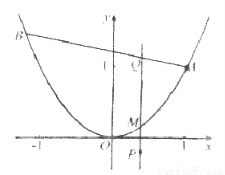
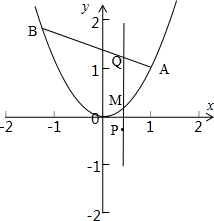设λ＞0，点A的坐标为（1，1），点B在抛物线y=x2上运动，点Q满足 |
| BQ |
|
| QA |
|
| QM |
|
| MP |
分析：设出点的坐标，利用向量的坐标公式求出向量的坐标，代入已知条件中的向量关系得到各点的坐标关系；表示出B点的坐标；将B的坐标代入抛物线方程求出p的轨迹方程．
解答：解：由
=λ
知Q，M，P三点在同一条垂直于x轴的直线上，故可设P（x，y），Q（x，y0），M（x，x2）则
x2-y0=λ（y-x2）即y0=（1+λ）x2-λy①
再设B（x1，y1）由
=λ
得
②
将①代入②式得
-λ(1+λ )y-λ③
又点B在抛物线y=x2
将③代入得（1+λ）2x2-λ（1+λ）y-λ=（（1+λ）x-λ）2
整理得2λ（1+λ）x-λ（1+λ）y-λ（1+λ）=0因为λ＞0所以2x-y-1=0
故所求的点P的轨迹方程：y=2x-1
| QM |
| MP |
x2-y0=λ（y-x2）即y0=（1+λ）x2-λy①
再设B（x1，y1）由
| BQ |
| QA |
|
将①代入②式得
|
又点B在抛物线y=x2
将③代入得（1+λ）2x2-λ（1+λ）y-λ=（（1+λ）x-λ）2
整理得2λ（1+λ）x-λ（1+λ）y-λ（1+λ）=0因为λ＞0所以2x-y-1=0
故所求的点P的轨迹方程：y=2x-1
点评：本题考查题中的向量关系提供点的坐标关系、求轨迹方程的重要方法：相关点法，即求出相关点的坐标，将相关点的坐标代入其满足的方程，求出动点的轨迹方程．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
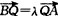，经过点Q与x轴垂直的直线交抛物线于点M，点P满足
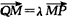，求点P的轨迹方程。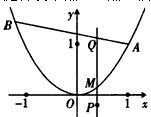
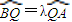，经过点Q与x轴垂直的直线交抛物线于点M，点P满足
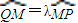，求点P的轨迹方程．