题目内容
(2008•深圳一模)在△ABC中,已知AC=3,sinA+cosA=
.
(Ⅰ)求sinA的值;
(Ⅱ)若△ABC的面积S=3,求BC的值.
| 2 |
(Ⅰ)求sinA的值;
(Ⅱ)若△ABC的面积S=3,求BC的值.
分析:(Ⅰ)由sinA+cosA=
sin(A+
)=
得sin(A+
)=1,由此能求出sinA的值.
(Ⅱ)由S=
bcsinA=
c=3得c=2
,由此及余弦定理能求出BC的值.
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
(Ⅱ)由S=
| 1 |
| 2 |
3
| ||
| 4 |
| 2 |
解答:解:(Ⅰ)由sinA+cosA=
sin(A+
)=
,
得sin(A+
)=1,
由此及0<A<π,即
<A+
<
得A+
=
,故A=
,
∴sinA=sin
=
;
(Ⅱ)由S=
bcsinA=
c=3,
得c=2
,
由此及余弦定理得a2=b2+c2-2bccosA=9+8-2×3×2
×
=5,
故a=
,即BC=
.
| 2 |
| π |
| 4 |
| 2 |
得sin(A+
| π |
| 4 |
由此及0<A<π,即
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
得A+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∴sinA=sin
| π |
| 4 |
| ||
| 2 |
(Ⅱ)由S=
| 1 |
| 2 |
3
| ||
| 4 |
得c=2
| 2 |
由此及余弦定理得a2=b2+c2-2bccosA=9+8-2×3×2
| 2 |
| ||
| 2 |
故a=
| 5 |
| 5 |
点评:本题考查两角和与两角差的正弦函数,解题时要认真审题,注意三角函数的恒等变换.

练习册系列答案
相关题目
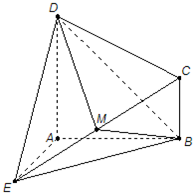 (2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.
(2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.