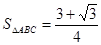题目内容
有一道解三角形的题,因为纸张破损,在划横线地方有一个已知条件看不清.具体如下:在△ABC中角A,B,C所对的边长分别为a,b,c,已知角B=45°,a=
,
| 3 |
c=
| ||||
| 2 |
c=
,求角A.若已知正确答案为A=60°,且必须使用所有已知条件才能解得,请你写出一个符合要求的已知条件.
| ||||
| 2 |
分析:只要知道了c边,使用所有已知条件才能解得此三角形,由于正确答案为 A=60°,故B=75°,根据正弦定理
=
,解得 c=
.
| ||
| sin60° |
| c |
| sin(45°+30°) |
| ||||
| 2 |
解答:解:根据题目的要求,只要知道了c边,使用所有已知条件才能解得此三角形,由于正确答案为 A=60°,故
B=75°=45°+30°,根据正弦定理
=
,解得 c=
.
故 一个符合要求的已知条件可以是 c=
,
故答案为:c=
.
B=75°=45°+30°,根据正弦定理
| ||
| sin60° |
| c |
| sin(45°+30°) |
| ||||
| 2 |
故 一个符合要求的已知条件可以是 c=
| ||||
| 2 |
故答案为:c=
| ||||
| 2 |
点评:本题考查正弦定理的应用,答案不唯一,得到
=
,是解题的关键.
| ||
| sin60° |
| c |
| sin(45°+30°) |

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
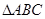 中角
中角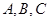 所对的边长分别为
所对的边长分别为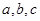 ,已知角
,已知角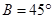 ,
,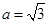 , ,求角
, ,求角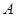 .若已知正确答案为
.若已知正确答案为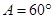 ,且必须使用所有已知条件才能解得,请你选出一个符合要求的已知条件.( )
,且必须使用所有已知条件才能解得,请你选出一个符合要求的已知条件.( ) B.
B.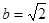
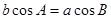 D.
D.