题目内容
有一道解三角形的题因纸张破损有一个条件不清,具体如下:在△ABC中,已知a=
,B=45°,
| 3 |
c=
| ||||
| 2 |
c=
,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=60°,试将条件在横线处补全.
| ||||
| 2 |
分析:要把横线处补全,就要把A的度数作为已知条件求c的值,由a,A和B的度数,根据正弦定理求出b的长,再由三角形的内角和定理求出C的度数,由a,b及cosC,利用余弦定理即可求出c的长.
解答:解:根据正弦定理得:
=
,a=
,sinB=
,sinA=
,
所以b=
=
,又C=180°-45°-60°=75°,
所以cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=
,
所以c2=a2+b2-2abcosC=3+2-2
×
=
=(
)2,
则c=
.
故答案为:c=
| a |
| sinA |
| b |
| sinB |
| 3 |
| ||
| 2 |
| ||
| 2 |
所以b=
| ||||||
|
| 2 |
所以cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=
| ||||
| 4 |
所以c2=a2+b2-2abcosC=3+2-2
| 6 |
| ||||
| 4 |
8+4
| ||
| 4 |
| ||||
| 2 |
则c=
| ||||
| 2 |
故答案为:c=
| ||||
| 2 |
点评:此题考查学生灵活运用正弦、余弦定理化简求值,灵活运用两角和与差的余弦函数公式化简求值,是一道中档题.把A的度数看做已知条件求c的长度是解本题的基本思路.

练习册系列答案
相关题目
 ,B=
,B= , ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=
, ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A= ,请将条件补完整.
,请将条件补完整.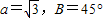 , ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=60°,试将条件在横线处补全.
, ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=60°,试将条件在横线处补全.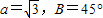 , ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=60°,试将条件在横线处补全.
, ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=60°,试将条件在横线处补全.