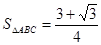题目内容
有一道解三角形的题,因为纸张破损,在划横线地方有一个已知条件看不清.具体如下:在△ABC中角A,B,C所对的边长分别为a,b,c,已知角B=45°,a=
,( ),求角A.若已知正确答案为A=60°,且必须使用所有已知条件才能解得,请你选出一个符合要求的已知条件.
| 3 |
分析:若给出的是角C,求角A用不到边a,若给出b=
,使用正弦定理求出的角A不唯一,由bcosA=acosB得到A=B,得到的角A不是60°,使用所有已知条件才能解得此三角形,由于正确答案为 A=60°,故B=75°,根据正弦定理
=
,解得c=
,此时由S△ABC=
acsinB算得S△ABC=
.
| 2 |
| ||
| sin60° |
| c |
| sin(45°+30°) |
| ||||
| 2 |
| 1 |
| 2 |
3+
| ||
| 4 |
解答:解:由于正确答案为 A=60°,故B=75°=45°+30°,
根据正弦定理
=
,解得c=
.
故一个符合要求的已知条件可以是c=
.
而选项中没有该选项,但由S△ABC=
,即
acsinB=
,
得c=
=
.
也就是给出S△ABC=
,使用所有已知条件能解出正确答案为A=60°.
故选:D.
根据正弦定理
| ||
| sin60° |
| c |
| sin(45°+30°) |
| ||||
| 2 |
故一个符合要求的已知条件可以是c=
| ||||
| 2 |
而选项中没有该选项,但由S△ABC=
3+
| ||
| 4 |
| 1 |
| 2 |
3+
| ||
| 4 |
得c=
| ||||||||||||||||
|
| ||||
| 2 |
也就是给出S△ABC=
3+
| ||
| 4 |
故选:D.
点评:本题考查正弦定理的应用,考查了逆向思维方法,利用
=
求解c是解题的关键,是中档题.
| ||
| sin60° |
| c |
| sin(45°+30°) |

练习册系列答案
相关题目
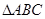 中角
中角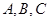 所对的边长分别为
所对的边长分别为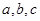 ,已知角
,已知角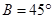 ,
,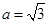 , ,求角
, ,求角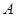 .若已知正确答案为
.若已知正确答案为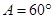 ,且必须使用所有已知条件才能解得,请你选出一个符合要求的已知条件.( )
,且必须使用所有已知条件才能解得,请你选出一个符合要求的已知条件.( ) B.
B.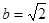
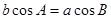 D.
D.