题目内容
（2011•成都模拟）已知F1、F2分别为椭圆
+
=1（a＞b＞0）的左右焦点，经过椭圆上第二象限内任意一点P的切线为l，过原点O作OM∥l交F2P于点M，则|MP|与a、b的关系是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
分析：设椭圆的左端点为A，考察特殊情形，当点P→A时，切线l→直线x=-a，此时|PM|→AO，即|PM|→a，对照选项得出答案．
解答：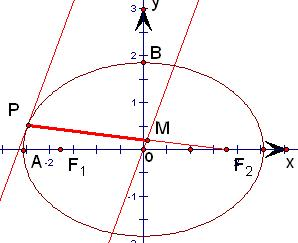
解：考察特殊情形，设椭圆的左端点为A，
当点P→A时，
切线l→直线x=-a，
此时|PM|→AO，
即|PM|→a，
特别地，当P与A重合时，|PM|=a．
对照选项，选A．
故选A．
解：考察特殊情形，设椭圆的左端点为A，当点P→A时，
切线l→直线x=-a，
此时|PM|→AO，
即|PM|→a，
特别地，当P与A重合时，|PM|=a．
对照选项，选A．
故选A．
点评：本小题主要考查椭圆的简单性质、椭圆的标准方程等基础知识，考查数形结合思想、极限思想．属于基础题．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目