Question

11．已知函数f（x）=$\left\{\begin{array}{l}{kx+1，x≤0}\\{lo{g}_{3}x，x＞0}\end{array}\right.$，下列函数y=f[f（x）]-$\frac{1}{2}$零点个数的四个判断：①当k＞0时，有3个零点；②当k＜0时，有2个零点；③当k＞0时，有4个零点④当k＜0时，有1个零点．则正确的判断是（　　）

• A． ①④
• B． ②③
• C． ①②
• D． ③④

Answer 1

分析 画出函数f（x）=$\left\{\begin{array}{l}{kx+1，x≤0}\\{lo{g}_{3}x，x＞0}\end{array}\right.$的图象，借助图象分析函数零点的个数，进而可得答案．

解答 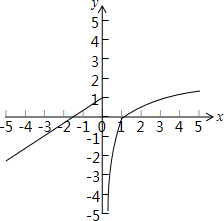解：函数f（x）=$\left\{\begin{array}{l}{kx+1，x≤0}\\{lo{g}_{3}x，x＞0}\end{array}\right.$的图象如右图所示：
结合图象分析：
当k＞0时，若y=f[f（x）]-$\frac{1}{2}$=0，则f[f（x）]=$\frac{1}{2}$，
则f（x）=a∈（-$\frac{1}{k}$，0）或f（x）=b∈（1，+∞），
对于f（x）=a，存在两个零点；
对于f（x）=b，存在一个零点，
综上所述，k＞0时，函数y=f[f（x）]-$\frac{1}{2}$零点个数为3个；
当k＜0时，若y=f[f（x）]-$\frac{1}{2}$=0，则f[f（x）]=$\frac{1}{2}$，
则由右图可知，f（x）=c∈（1，+∞），
对于f（x）=c，存在两个零点，
当k＜0时，有2个零点．
故选：C．

点评 本题考查的知识点是函数的零点，分段函数的图象，对数函数的图象和性质，一次函数的图象和性质，注意运用数形结合思想，难度中档．