题目内容
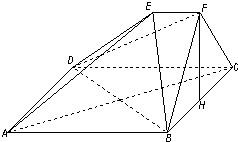 如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF,∠BFC=90°,BF=FC,H为BC的中点.
如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF,∠BFC=90°,BF=FC,H为BC的中点.(1)求证:FH∥平面EDB;
(2)求证:AC⊥平面EDB;
(3)求二面角B-DE-C的大小.
分析:(1)设AC于BD交于点G,则G为AC的中点,连接EG,GH,又H为BC的中点,可得四边形EFHG为平行四边形,然后利用直线与平面平行判断定理进行证明;
(2)因为四边形ABCD为正方形,有AB⊥BC,又EF∥AB,可得EF⊥BC,要证FH⊥平面ABCD,FH⊥平面ABCD,从而求解.
(3)在平面CDEF内过点F作FK⊥DE交DE的延长线与k,可知∠FKB为二面角B-DE-C的一个平面角,然后设EF=1,在直角三角形中进行求证.
(2)因为四边形ABCD为正方形,有AB⊥BC,又EF∥AB,可得EF⊥BC,要证FH⊥平面ABCD,FH⊥平面ABCD,从而求解.
(3)在平面CDEF内过点F作FK⊥DE交DE的延长线与k,可知∠FKB为二面角B-DE-C的一个平面角,然后设EF=1,在直角三角形中进行求证.
解答:证明:(1)设AC于BD交于点G,则G为AC的中点,连接EG,GH,又H为BC的中点,
∴GH∥AB且GH=
AB,又EF∥AB且EF=
AB,∴EF∥GH且EF=GH,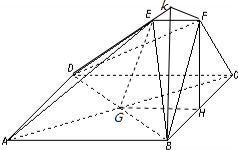
∴四边形EFHG为平行四边形
∴EG∥FH,而EG?平面EDB,∴FH∥平面EDB.
(2)由四边形ABCD为正方形,有AB⊥BC,又EF∥AB,∴EF⊥BC
而EF⊥FB,∴EF⊥平面BFC,∴EF⊥FH,∴AB⊥FH,
又BF=FC,H为BC的中点,∴FH⊥BC
∴FH⊥平面ABCD,∴FH⊥BC,FH⊥AC,
又FH∥EG,∴AC⊥EG
又AC⊥BD,EG∩BD=G,
∴AC⊥平面EDB,
(3)EF⊥FB,∠BFC=90°,∴BF⊥平面CDEF,
在平面CDEF内过点F作FK⊥DE交DE的延长线与k,则
∠FKB为二面角B-DE-C的一个平面角,
设EF=1,则AB=2,FC=
,DE=
,
又EF∥DC,∴∠KEF=∠EDC,
∴sin∠EDC=sin∠KEF=
,
∴FK=EFsin∠KEF=
,
tan∠FKB=
=
,
∴∠FKB=60°,
∴二面角B-DE-C为60°.
∴GH∥AB且GH=
| 1 |
| 2 |
| 1 |
| 2 |

∴四边形EFHG为平行四边形
∴EG∥FH,而EG?平面EDB,∴FH∥平面EDB.
(2)由四边形ABCD为正方形,有AB⊥BC,又EF∥AB,∴EF⊥BC
而EF⊥FB,∴EF⊥平面BFC,∴EF⊥FH,∴AB⊥FH,
又BF=FC,H为BC的中点,∴FH⊥BC
∴FH⊥平面ABCD,∴FH⊥BC,FH⊥AC,
又FH∥EG,∴AC⊥EG
又AC⊥BD,EG∩BD=G,
∴AC⊥平面EDB,
(3)EF⊥FB,∠BFC=90°,∴BF⊥平面CDEF,
在平面CDEF内过点F作FK⊥DE交DE的延长线与k,则
∠FKB为二面角B-DE-C的一个平面角,
设EF=1,则AB=2,FC=
| 2 |
| 3 |
又EF∥DC,∴∠KEF=∠EDC,
∴sin∠EDC=sin∠KEF=
| ||
|
∴FK=EFsin∠KEF=
| ||
|
tan∠FKB=
| BF |
| FK |
| 3 |
∴∠FKB=60°,
∴二面角B-DE-C为60°.
点评:此题考查直线与平面平行的判断及平面与平面垂直的判断,此类问题一般先证明两个面平行,再证直线和面平行,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,同学们要课下要多练习.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC, (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC, (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=