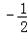题目内容
若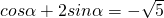 ,则tanα=
,则tanα=
- A.

- B.2
- C.

- D.-2
B
分析:本小题主要考查三角函数的求值问题,需要把正弦和余弦化为正切和正割,两边平方,根据切割的关系进行切割互化,得到关于正切的方程,解方程得结果.
解答:∵cosα+2sinα=- ,
,
∴cosα≠0,
两边同时除以cosα得1+2tanα=- ,
,
∴(1+2tanα)2=5sec2α=5(1+tan2α),
∴tan2α-4tanα+4=0,
∴tanα=2.
故选B.
点评:同角三角函数之间的关系,其主要应用于同角三角函数的求值和同角三角函数之间的化简和证明.在应用这些关系式子的时候就要注意公式成立的前提是角对应的三角函数要有意义.熟记这几个公式是能应用的前提,把它们分为三类记住.
分析:本小题主要考查三角函数的求值问题,需要把正弦和余弦化为正切和正割,两边平方,根据切割的关系进行切割互化,得到关于正切的方程,解方程得结果.
解答:∵cosα+2sinα=-
 ,
,∴cosα≠0,
两边同时除以cosα得1+2tanα=-
 ,
,∴(1+2tanα)2=5sec2α=5(1+tan2α),
∴tan2α-4tanα+4=0,
∴tanα=2.
故选B.
点评:同角三角函数之间的关系,其主要应用于同角三角函数的求值和同角三角函数之间的化简和证明.在应用这些关系式子的时候就要注意公式成立的前提是角对应的三角函数要有意义.熟记这几个公式是能应用的前提,把它们分为三类记住.

练习册系列答案
相关题目
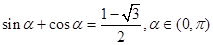 ,则tan
,则tan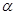 =
=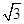 B.
B.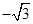 C.
C.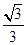 D.
D.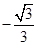
 ,则tanθ=
,则tanθ=

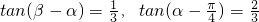 ,则tanβ=
,则tanβ=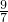
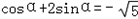 ,则tan
,则tan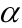 =
=