题目内容
已知Sn是等差数列{an}(nÎN*)的前n项和,且S6>S7>S5,有下列四个命题,假命题的是( )
| A.公差d<0 | B.在所有Sn<0中,S13最大 |
| C.满足Sn>0的n的个数有11个 | D.a6>a7 |
C
解析试题分析:∵等差数列{an}中,S6最大,且S6>S7>S5∴a1>0,d<0,A正确;
∵S6最大,a6>0,a7<0,∴D正确;
∵S13=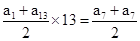 ×13<0,
×13<0,
∵a6+a7>0,a6>-a7,s12= >0;
>0;
∴Sn的值当n≤6递增,当n≥7递减,前12项和为正,当n=13时为负.
故B正确;满足sn>0的n的个数有12个,故C错误;
故选C。
考点:本题主要考查等差数列的通项公式、求和公式。
点评:典型题,在等差数列中Sn存在最大值的条件是:a1>0,d<0.一般两种解决问题的思路:“项分析法”与“和分析法”。

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
等差数列的前n项和为Sn,而且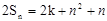 ,则常数k的值为( )
,则常数k的值为( )
| A.1 | B.-1 | C.1 | D.0 |
设等差数列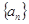 的前n项和为
的前n项和为 ,已知
,已知 ,
,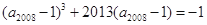 则下列结论中正确的是( )
则下列结论中正确的是( )
A. | B.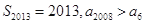 |
C.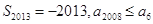 | D.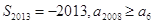 |
等差数列-5,-2,1,…的前20项的和为( )
| A.450 | B.470 | C.490 | D.510 |
等差数列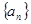 的前
的前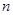 项和为
项和为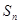 ,若
,若 ,则
,则 ( )
( )
| A.18 | B.36 | C.45 | D.60 |
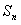 是等差数列
是等差数列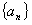 的前
的前 项和,若
项和,若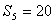 ,则
,则 ( )
( )
| A.15 | B.18 | C.9 | D.12 |
已知等差数列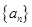 的前项和为
的前项和为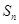 ,且
,且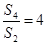 ,则
,则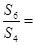 ( )
( )
A.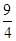 | B.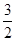 | C.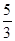 | D.4 |
等差数列{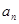 }中,
}中,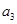 =2,
=2,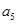 =7,则
=7,则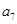 =
=
| A.10 | B.20 | C.16 | D.12 |
已知等差数列{an}满足a2=3,Sn-Sn-3=51(n>3) ,Sn= 100,则n的值为
| A.8 | B.9 | C.10 | D.11 |