题目内容
等差数列的前n项和为Sn,而且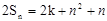 ,则常数k的值为( )
,则常数k的值为( )
| A.1 | B.-1 | C.1 | D.0 |
D
解析试题分析:根据题意,由于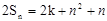 ,那么可知根据其与二次函数的特点可知,前n项和是关于过原点的二次函数,因此常数项为0,可知,2k=0,得到k=0,故选D.
,那么可知根据其与二次函数的特点可知,前n项和是关于过原点的二次函数,因此常数项为0,可知,2k=0,得到k=0,故选D.
考点:等差数列的前n项和
点评:主要是考查了等差数列的前n项和的由于,属于基础题。

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
在等差数列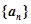 中,若
中,若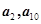 是方程
是方程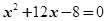 的两个根,那么
的两个根,那么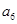 的值为( )
的值为( )
| A.-6 | B.-12 | C.12 | D.6 |
设等差数列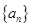 满足
满足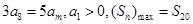 ,则m的值为
,则m的值为
A.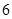 | B.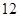 | C. | D.26 |
等差数列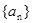 中,
中, ,则
,则 ( )
( )
A. | B.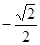 | C. 0 | D.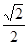 |
在等差数列 中,
中,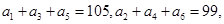 以
以 表示数列
表示数列 的前
的前 项和,则使
项和,则使 达到最大值的
达到最大值的 是( )
是( )
A.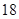 | B.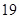 | C.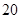 | D.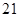 |
已知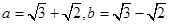 ,则
,则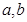 的等差中项为( )
的等差中项为( )
A.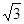 | B.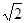 | C.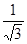 | D.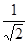 |
等差数列 前
前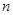 项和
项和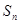 ,
,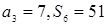 ,则公差d的值为 ( )
,则公差d的值为 ( )
| A.2 | B.3 | C.4 | D.-3 |
若Sn是等差数列{an}的前n项和,a2+a10=4,则S11的值为
| A.12 | B.18 | C.22 | D.44 |
已知Sn是等差数列{an}(nÎN*)的前n项和,且S6>S7>S5,有下列四个命题,假命题的是( )
| A.公差d<0 | B.在所有Sn<0中,S13最大 |
| C.满足Sn>0的n的个数有11个 | D.a6>a7 |