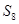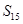题目内容
设等差数列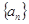 的前n项和为
的前n项和为 ,已知
,已知 ,
,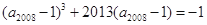 则下列结论中正确的是( )
则下列结论中正确的是( )
A. | B.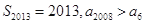 |
C.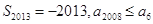 | D.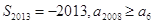 |
A
解析试题分析:由于 ,
,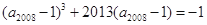 ,可知
,可知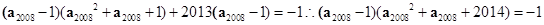 ,且有
,且有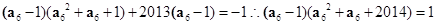 ,两式相加得到为零,那么可以推理得到
,两式相加得到为零,那么可以推理得到 ,选A.
,选A.
考点:数列的通项公式和求和
点评:解决的关键是通过已知的数列的关系式得到函数与方程的根来得到求解,属于基础题。

练习册系列答案
相关题目
设等差数列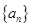 满足
满足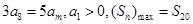 ,则m的值为
,则m的值为
A.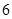 | B.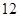 | C. | D.26 |
等差数列 前
前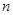 项和
项和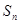 ,
,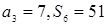 ,则公差d的值为 ( )
,则公差d的值为 ( )
| A.2 | B.3 | C.4 | D.-3 |
若Sn是等差数列{an}的前n项和,a2+a10=4,则S11的值为
| A.12 | B.18 | C.22 | D.44 |
已知等差数列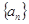 中
中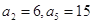 ,若
,若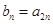 ,则数列
,则数列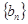 的前
的前 项和等于( )
项和等于( )
A.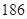 | B. | C.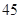 | D.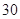 |
各项均为正数的等比数列{ }的公比q≠1,且a2,
}的公比q≠1,且a2, a3,a1成等差数列,则
a3,a1成等差数列,则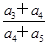 的值是
的值是
A.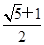 | B. | C.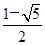 | D.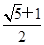 或 或 |
已知Sn是等差数列{an}(nÎN*)的前n项和,且S6>S7>S5,有下列四个命题,假命题的是( )
| A.公差d<0 | B.在所有Sn<0中,S13最大 |
| C.满足Sn>0的n的个数有11个 | D.a6>a7 |
在等差数列{an}中,已知a4+a8=16,则该数列前11项和S11=( )
| A.58 | B.88 | C.143 | D.176 |
 的公差为
的公差为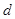 ,前
,前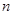 项和为
项和为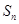 ,当首项
,当首项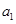 和
和 是一个定值,则下列各数中也为定值的是 ( )
是一个定值,则下列各数中也为定值的是 ( )